Question

Find the indicated partial derivatives. f(x, y) = arctan(y/x); fx(−5, −5) fx(−5, −5) = ?

Answer 1

To find the partial derivative fx of the given function f(x, y), we differentiate the function with respect to x while treating y as a constant. Substituting the given values, fx(-5, -5) = 1/10.

Step-by-step explanation:

To find the partial derivative of a function, we need to take the derivative with respect to the specified variable while treating all other variables as constants.

In this case, we need to find the partial derivative of f(x, y) with respect to x.

The function is given as f(x, y) = arctan(y/x).

To find fx, we differentiate the function with respect to x while treating y as a constant.

Therefore,
`fx = -y/(x^2 + y^2).`

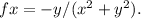
Substituting the values x = -5 and y = -5 into fx, we get fx(-5, -5)

`= -(-5)/((-5)^2 + (-5)^2)`

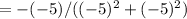
= 5/(25 + 25)

= 5/50

= 1/10.