Question

Question Workspace Check My Work Wendy's restaurant has been recognized for having the fastest average service time among fast food restaurants. In a benchmark study, Wendy's average service time of 2.2 minutes was less than those of Burger King, Chick-fil-A, Krystal, McDonald's, Taco Bell, and Taco John's (QSR Magazine website, December 2014). Assume that the service time for Wendy's has an exponential distribution. a. What is the probability that a service time is less than or equal to one minute (to 4 decimals)?

Answer 1

The probability that a Wendy's service time is less than or equal to one minute is approximately 36.53%, calculated using the exponential distribution formula.

Step-by-step explanation:

To calculate the probability that a service time at Wendy's is less than or equal to one minute, given an exponential distribution with an average service time of 2.2 minutes, we use the formula for the exponential distribution: P(X <= x) = 1 -
`e^{(-\lambda \space x)`, where λ is the rate parameter, which is the reciprocal of the mean service time, and x is the time we are interested in. First, calculate the rate parameter (λ = 1/2.2). Then use the x value of one minute to find the probability:

λ = 1 / 2.2 = 0.4545 (to 4 decimal places)

Therefore:

`P(X < = 1) = 1 - e^((-0.4545* 1)) = 1 - e^((-0.4545)) \approx 1 - 0.6347 \approx 0.3653`

So, the probability that a service time is less than or equal to one minute is approximately 0.3653 or 36.53%.

Answer 2

The probability that a service time at Wendy's is less than or equal to one minute is calculated using the exponential distribution's PDF. For Wendy's, with an average service time of 2.2 minutes, the result for this probability is
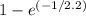`1 - e^((-1/2.2))`. Similarly, the average minutes between successive arrivals is 2.2 minutes, and for three customers to arrive, it's expected to be 6.6 minutes.

Step-by-step explanation:

For Wendy's restaurant, if the service time has an exponential distribution with an average service time of 2.2 minutes, we can use the exponential probability density function (PDF) to calculate the probability that a service time is less than or equal to one minute. The PDF for an exponentially distributed random variable X is given by
`f(x) = λ * e^((-λx))`, where λ = 1/μ and μ is the average service time. For Wendy's, λ = 1/2.2. Therefore, the probability that a service time is less than or equal to one minute is the integral of f(x) from 0 to 1, which equals
`1 - e^((-1/2.2))`.

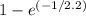To find the probability that it takes less than one minute for the next customer to arrive, we can use the same exponential PDF since the arrival times are also exponentially distributed. Using the function f(x) as defined above, we compute
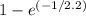`1 - e^((-1/2.2))` to get this probability.

Similarly, the probability that it takes more than five minutes for the next customer to arrive is found using the complement of the cumulative distribution function (CDF) for x = 5, which is
`e^((-5/2.2))`.

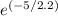For the average time between successive customer arrivals, we refer back to the mean of the exponential distribution, which is the reciprocal of the rate λ. So the average time between two successive arrivals at Wendy's is 2.2 minutes. When the store first opens, it will take, on average, 2.2 * 3 = 6.6 minutes for three customers to arrive.