Question

. A 90-kg man stands in an elevator that is moving up at a constant speed of 5.0 m/s. The force exerted by him on the floor is about: A) 0 N B) 90 N C) 880 N D) 450 N E) 1330 N

Answer 1

Approximately
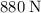`880\; {\rm N}`, assuming that
`g = 9.81\; {\rm N \cdot kg^(-1)}` and that the floor of the elevator is level.

Step-by-step explanation:

The forces on this person are:

• Weight, which points downward, and
• Normal force from the floor, which points downward.

The vector sum of these two forces is equal to the net force on this person:

`(\text{net force}) = (\text{weight}) + (\text{normal force})`.

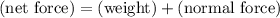Rearrange to find the normal force:

`(\text{normal force}) = (\text{net force}) - (\text{weight})`.

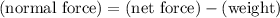Since the mass of this person is
`m = 90\; {\rm kg}`, the weight of this person would be:

`\begin{aligned}(\text{weight}) &= m\, (-g) \\ &= (90\; {\rm kg})\, ((-9.81)\; {\rm N\cdot kg^(-1)})\\ &\approx (-880)\; {\rm N}\end{aligned}`.

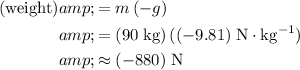(Negative because weight points downwards.)

It is given that this person is moving at a constant speed. In other words, the acceleration of this person is
`a = 0\; {\rm m\cdot s^(-2)}`, and this person is in a translational equilibrium. By Newton's Laws of Motion, the net force on this person would be
`0\: {\rm N}`:

`\begin{aligned} (\text{net force}) &= m\, a \\ &= (90\; {\rm kg}) \, (0\; {\rm m\cdot s^(-2)}) \\ &= 0\: {\rm N} \end{aligned}`.

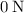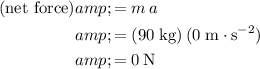Substitute this value into the expression for the normal force on this person:

`\begin{aligned} (\text{normal force}) &= (\text{net force}) - (\text{weight}) \\ &\approx 0\; {\rm N} - ((-880)\; {\rm N}) \\ &= 880\; {\rm N}\end{aligned}`.

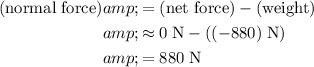The question is asking for the force that this person exerts on the floor, which is the reaction force to the normal force the floor exerts on this person. By Newton's Laws of motion, these two forces would be equal in magnitude. Hence, the magnitude of the force that this person exerts on the floor would also be approximately
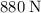`880\; {\rm N}`.