Question

Find the slope of a line perpendicular to the line y=-1/4x-1

Answer 1

The idea is that perpendicular lines have slopes that are opposite reciprocals. So, this means that to find the slope of a line that is perpendicular to another one we should flop it and change its sign.

Given line

`\sf{y=-\cfrac{1}{4}x-1}`

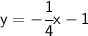
Its slope (the number before x) :

`\sf{-\cfrac{1}{4}}`

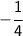
Flopping it :

`\sf{-\cfrac{4}{1}}`, which is -4

Changing the sign :

4

Therefore, the slope is 4.

Answer 2

To find the slope of a line perpendicular to the line y = -1/4x - 1, you can use the fact that the slopes of perpendicular lines are negative reciprocals of each other.

The given line has a slope of -1/4. To find the slope of a line perpendicular to it, take the negative reciprocal of -1/4:

Slope of the perpendicular line = -1 / (-1/4) = -1 / (-1/4) * (4/4) = 4

So, the slope of a line perpendicular to the line y = -1/4x - 1 is 4.