The value for q of the reaction is approximately 3.54 times
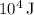 (rounded to three significant figures and in scientific notation).
(rounded to three significant figures and in scientific notation).
To calculate the heat (\( q \)) of the reaction, you can use the formula:
![\[ q = mc\Delta T \]](https://img.qammunity.org/2024/formulas/physics/high-school/ltij11nchnq47mlyrpofeis7ug352gt24k.png)
where:
q is the heat,
m is the mass,
-c is the specific heat capacity, and
 is the change in temperature.
is the change in temperature.
Given values:
Mass of water
 : 950 g
: 950 g
Specific heat capacity of water
 : 4.18 J/g°C
: 4.18 J/g°C
Change in temperature (
 :
:
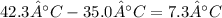
First, calculate the heat
 absorbed by the water:
absorbed by the water:
![\[ q_1 = m \cdot c \cdot \Delta T \]](https://img.qammunity.org/2024/formulas/chemistry/college/txf4bbth6iiinjr17bssy178pgvb79jg0w.png)
![\[ q_1 = (950 \, \text{g}) \cdot (4.18 \, \text{J/g°C}) \cdot (7.3°C) \]](https://img.qammunity.org/2024/formulas/chemistry/college/nkuti2vjb2efscb4vw77xfcv460tk8p3md.png)
Now, calculate the heat
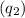 released by the bomb calorimeter:
released by the bomb calorimeter:
![\[ q_2 = C \cdot \Delta T \]](https://img.qammunity.org/2024/formulas/chemistry/college/sskury2oy4nascneah6y7fs2jnfj59n9rg.png)
![\[ q_2 = (933 \, \text{J/°C}) \cdot (7.3°C) \]](https://img.qammunity.org/2024/formulas/chemistry/college/io3af8qf3gxw2mmeh6r8omxfm2jgbuv5b8.png)
The total heat (\( q \)) of the reaction is the sum of
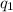 and
and
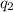 :
:
![\[ q = q_1 + q_2 \]](https://img.qammunity.org/2024/formulas/chemistry/college/fvnskx6xga1y3uwi0d5ccgb0jwxczz7l16.png)
Now, calculate q using the given values:
![\[ q = (950 \, \text{g}) \cdot (4.18 \, \text{J/g°C}) \cdot (7.3°C) + (933 \, \text{J/°C}) \cdot (7.3°C) \]](https://img.qammunity.org/2024/formulas/chemistry/college/mvxo5t5euxzs871s6lv3cyvvnlaoghiqkh.png)
Let's calculate the expression:
![\[ q = (950 \, \text{g}) \cdot (4.18 \, \text{J/g°C}) \cdot (7.3°C) + (933 \, \text{J/°C}) \cdot (7.3°C) \]](https://img.qammunity.org/2024/formulas/chemistry/college/mvxo5t5euxzs871s6lv3cyvvnlaoghiqkh.png)
![\[ q = (950 \, \text{g}) \cdot (4.18 \, \text{J/g°C}) \cdot (7.3°C) + (933 \, \text{J/°C}) \cdot (7.3°C) \]](https://img.qammunity.org/2024/formulas/chemistry/college/mvxo5t5euxzs871s6lv3cyvvnlaoghiqkh.png)
Now, perform the calculations:
![\[ q \approx 28564.82 \, \text{J} + 6815.9 \, \text{J} \]](https://img.qammunity.org/2024/formulas/chemistry/college/sjnwmrqeqtkkaulsz1ayqweaom40em1f3u.png)
![\[ q \approx 35380.72 \, \text{J} \]](https://img.qammunity.org/2024/formulas/chemistry/college/7shxt3fhfrtg6iegt87hfrmxwsomcfns3t.png)
Now, express the result in scientific notation with three significant figures:
![\[ q \approx 3.54 * 10^4 \, \text{J} \]](https://img.qammunity.org/2024/formulas/chemistry/college/q2ka55fa53idfpowfmrdjhrauxc83f09d3.png)