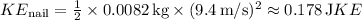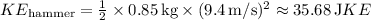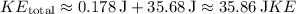Question

Calculate the kinetic energy acquired by a 8.2-gg nail when it is struck by a 850-gg hammer moving with an initial speed of 9.4 m/sm/s. Express your answer using two significant figures.

Answer 1

The kinetic energy acquired by the nail is 0.00037 joules.

Step-by-step explanation:

The kinetic energy acquired by the nail can be calculated using the formula:

K.E. = (1/2) * m * v²,

where m is the mass of the nail and v is its velocity. In this case, the mass of the nail is 8.2 g and the velocity is the same as that of the hammer, which is 9.4 m/s. Converting the mass to kilograms: 8.2 g = 0.0082 kg.

By substituting the values into the formula, we get:
K.E. = (1/2) * 0.0082 kg * (9.4 m/s)²

K.E. = 0.00037 J.

Therefore, the kinetic energy acquired by the nail is 0.00037 joules.

Answer 2

The kinetic energy acquired by the nail when struck by the hammer is approximately 35.86J (rounded to two significant figures).

To calculate the kinetic energy acquired by the nail when struck by the hammer, you can use the formula for kinetic energy:

`\[ KE = (1)/(2) m v^2 \]`

where:

KE is the kinetic energy,

m is the mass,

v is the velocity.

Let's convert the masses from grams to kilograms (1 g = 0.001 kg) and then use the formula:

Mass of the nail
`(\( m_{\text{nail}} \))` = 8.2 g = 0.0082 kg

Mass of the hammer
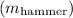`(\( m_{\text{hammer}} \))` = 850 g = 0.85 kg

Velocity
`(\( v \))` = 9.4 m/s

Now, plug in these values into the kinetic energy formula:

`\[ KE_{\text{nail}} = (1)/(2) * 0.0082 \, \text{kg} * (9.4 \, \text{m/s})^2 \]`

`\[ KE_{\text{hammer}} = (1)/(2) * 0.85 \, \text{kg} * (9.4 \, \text{m/s})^2 \]`

Add the two kinetic energies to get the total kinetic energy acquired by the nail:

`\[ KE_{\text{total}} = KE_{\text{nail}} + KE_{\text{hammer}} \]`

Let's calculate these values:

`KE_{\text{nail}} = (1)/(2) * 0.0082 \, \text{kg} * (9.4 \, \text{m/s})^2 \approx 0.178 \, \text{J}KE`

`KE_{\text{hammer}} = (1)/(2) * 0.85 \, \text{kg} * (9.4 \, \text{m/s})^2 \approx 35.68 \, \text{J}KE`

`KE_{\text{total}} \approx 0.178 \, \text{J} + 35.68 \, \text{J} \approx 35.86 \, \text{J}KE`