Question

a disk of mass 2.5 kg and radius 70 cm is rotating at 1.9 rev/s. a small mass of 0.07 kg drops onto the edge of the disk. what is the disk's final rotation rate

Answer 1

The disk's final rotation rate after the small mass is dropped onto its edge is approximately 1.815 revolutions per second.

what is the disk's final rotation rate

Given:

Mass of the disk (m₁) = 2.5 kg

Radius of the disk (r₁) = 70 cm = 0.7 m

Initial angular velocity of the disk (ω₁) = 1.9 rev/s

Mass dropped onto the edge (m₂) = 0.07 kg

We need to find the final rotation rate of the disk after the small mass is dropped onto its edge.

First, calculate the initial moment of inertia (I₁) of the disk:

`I_1 = (1/2) * m_1 * r_1^2\\= (1/2) * 2.5 kg * (0.7 m)^2\\= 0.6125 kg m^2`

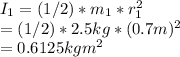
Next, determine the moment of inertia (I₂) after the mass is dropped onto the edge:

`I2 = I_1 + m_2 * r_1^2\\= 0.6125 kg m^2 + 0.07 kg * (0.7 m)^2\\= 0.6125 kg m^2 + 0.0343 kg m^2\\= 0.6468 kg m^2`

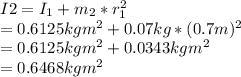
Now, apply the conservation of angular momentum:

I₁ * ω₁ = I₂ * ω₂

Solve for ω₂:

ω₂ = (I₁ * ω₁) / I₂

`= (0.6125 kg m^2 * 1.9 rev/s) / 0.6468 kg m^2`

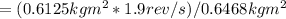
≈ 1.815 rev/s

Therefore, the disk's final rotation rate after the small mass is dropped onto its edge is approximately 1.815 revolutions per second.