Question

Strings are wound around two identical pucks: one is around its outer rim; the other is around its axle. You pull both pucks from rest by using the same force F. Both pucks start to move on a frictionless surface. 5 seconds later, which puck has greater rotational kinetic energy

Answer 1

After 5 seconds, the puck with the string wound around its outer rim will have greater rotational kinetic energy compared to the puck with the string wound around its axle, due to its larger moment of inertia.

Step-by-step explanation:

The question pertains to the rotational kinetic energy of two identical pucks that are pulled by the same force but differ in the point at which the force is applied. Using principles of physics, specifically moment of inertia and rotational dynamics, we can deduce that the puck with the string wound around its outer rim will have a larger moment of inertia compared to the puck with the string wound around its axle. Given the same torque produced by force F, and considering torque is equal to the product of the force and the radius at which it is applied, the puck with the larger radius (outer rim) will experience a lower angular acceleration due to its higher moment of inertia. However, both will have the same angular displacement after 5 seconds given the same angular acceleration over time. Therefore, knowing that rotational kinetic energy is given by (1/2)*I*ω^2 (where I is the moment of inertia and ω is angular velocity), and both pucks have the same angular velocity, the puck with the larger moment of inertia (around the outer rim) will have greater rotational kinetic energy after 5 seconds.

Answer 2

5 seconds later, the puck with the string wound around its outer rim will have greater rotational kinetic energy

To determine which puck has greater rotational kinetic energy after 5 seconds, we need to consider how the force applied affects the rotational motion of each puck. The key concept here is the relation between torque, angular acceleration, and rotational kinetic energy.

1. Torque and Angular Acceleration:

- Torque
`(\( \tau \)) is given by \( \tau = r * F \),` where r is the radius at which the force is applied and F is the force.

- Since both pucks are identical and the same force is applied, the one with a larger radius of application of the force (the puck with the string around its outer rim) will experience a greater torque because
`\( \tau = r * F \).`

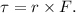
- Angular acceleration
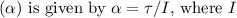`(\( \alpha \)) is given by \( \alpha = \tau / I \), where \( I \)`is the moment of inertia of the puck. Since the pucks are identical, they have the same moment of inertia. Thus, the puck with greater torque (the one with the string around its outer rim) will have a greater angular acceleration.

2. Rotational Kinetic Energy:

- Rotational kinetic energy
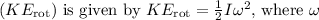`(\( KE_{\text{rot}} \)) is given by \( KE_{\text{rot}} = (1)/(2) I \omega^2 \), where \( \omega \)`is the angular velocity.

- Angular velocity after a certain time t can be found using
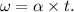`\( \omega = \alpha * t \).`Since the angular acceleration
`(\( \alpha \))`is greater for the puck with the string around its outer rim, it will have a greater angular velocity after the same time period.

3. Conclusion:

- After 5 seconds, the puck with the string wound around its outer rim will have a greater angular velocity due to the larger torque and angular acceleration it experiences.

- Consequently, this puck will have a greater rotational kinetic energy, as
`\( KE_{\text{rot}} \)`is directly proportional to the square of the angular velocity..