Question

A right pyramid has a base that is a square whose area is approximately 85.56 cm2. If the slant height of the pyramid is 12 cm, find the volume of the pyramid. A. 315.8 cm3 B. 218.02 cm3 C. 654.06 cm3 D. 342.24 cm3

Answer 1

Explanation:

Find the perpendicular height by creating a cross-section of the pyramid.

The hypotenuse will be 12 as this is the slant height.

The length of 1 side of the base will be
`√(85.56) = 9.249864864..`

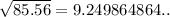
This means that the base of the right-angle triangle will be
`9.249864864 / 2 = 4.624932432`

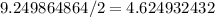
Use pythagoras' theoreom to find the perpendicular height:

`12^(2) - 4.624932432^(2) = √(122.61) = 11.07294`

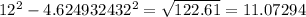
Use the volume of a pyramid formula to find volume:

Volume of pyramid =
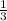`(1)/(3)` x base area x perpendicular height

Volume of pyramid =
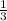`(1)/(3)` x 85.56 x 11.07294

Volume of pyramid = 315.8
`cm^3`

Hence, the answer is A.