Question

An object of mass M is attached to a string of negligible mass and spun in a vertical circle of radius R, ​ as shown in the figure below. As the object's height increases, its speed decreases such that the object-Earth system'stotal mechanical energy remains constant. By how much does the object's kinetic energy decrease in moving from point O, the lowest point on the circle, to point P the highest point on the circle? a. MgR/2 b. MgR c. MgR/4 d. 2mgR

Answer 1

The correct answer is c. MgR.

At the bottom of the circle (point O), the object has maximum kinetic energy and zero gravitational potential energy.

As the object moves up the circle, its kinetic energy decreases and its gravitational potential energy increases.

At the top of the circle (point P), the object has minimum kinetic energy and maximum gravitational potential energy.

Since the total mechanical energy of the system remains constant, the decrease in kinetic energy must be equal to the increase in gravitational potential energy.

The gravitational potential energy at point P is given by:

GPE = Mgh, where M is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above the lowest point.

In this case, the height h is equal to the radius of the circle (R). Therefore:

GPE = Mgr

The decrease in kinetic energy from point O to point P is therefore:

`ΔKE = KE_O - KE_P = (1/2)Mv^2_O - 0 = (1/2)Mv^2_O`

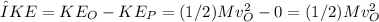
Setting the decrease in kinetic energy equal to the increase in gravitational potential energy:

`(1/2)Mv^2_O = Mgr`

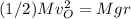
Solving for
`v^2_O`:

`v^2_O = 2gR`

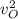Therefore, the decrease in kinetic energy is:

ΔKE =
`(1/2)M(2gR)`= MgR

So, the object's kinetic energy decreases by MgR in moving from point O to point P.

The other answer choices are incorrect because:

a. MgR/2: This is half of the correct answer. The gravitational potential energy increases by the full MgR, not half of it.

b. MgR/4: This is one-quarter of the correct answer. The gravitational potential energy increases by the full MgR, not one-quarter of it.

d. 2mgR: This is double the correct answer. The gravitational potential energy increases by MgR, not 2MgR.

I hope this explanation helps! Let me know if you have any other questions.