Question

A family has three girls and two boys. To select two children to do the dishes, the mother puts the names of the children on separate pieces of paper, mixes them up, and randomly draws two different pieces of paper, one at a time. What is the probability that they are both girls?

Answer 1

`(3)/(10)`

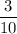
Explanation:

Probability is a measure of the likelihood or chance that an event will occur, expressed as a number between 0 (impossible) and 1 (certain).

`\boxed{\sf Probability\:of\:an\:event\:occurring = (Number\:of\:ways\:it\:can\:occur)/(Total\:number\:of\:possible\:outcomes)}`

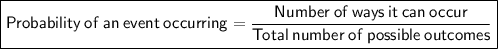
If a family has 3 girls and 2 boys, then the total number of possible outcomes is 5. To find the probability that the first child picked is a girl, divide the number of girls (3) by the total number of children (5):

`\textsf{P(First child is a girl)}=(3)/(5)`

As the pieces of paper are not replaced once they are picked, there are now a total of 4 children to choose from: 2 girls and 2 boys. Therefore, the probability that the second child picked is a girl is:

`\textsf{P(Second child is a girl)}=(2)/(4)=(1)/(2)`

To find the probability of both events happening (both children drawn are girls), multiply the probabilities of each event:

`\textsf{P(Both children are girls)}=(3)/(5)*(1)/(2)=(3)/(10)`

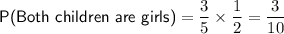
Therefore, the probability that both names of the children drawn are girls is 3/10.