Question

Solve 6 |3-k| + 14 > 14. Graph solution of absolute value.

Answer 1

k < 3 or k > 3

Explanation:

Given absolute value inequality:

`6 |3-k| + 14 > 14`

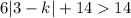
Subtract 14 from both sides:

`\begin{aligned}6 |3-k| + 14-14& > 14-14\\\\6|3-k|& > 0\end{aligned}`

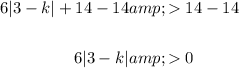
Divide both sides by 6:

`\begin{aligned}(6|3-k|)/(6)& > (0)/(6)\\\\|3-k|& > 0\end{aligned}`

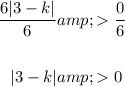
Apply the absolute rule:

`\boxed{\textsfIf\;$}`

`\begin{aligned}3-k& < 0\\3-k+k& < 0+k\\3& < k\\k& > 3\end{aligned}`
`\begin{aligned}3-k& > 0\\3-k+k& > 0+k\\3& > k\\k& < 3\end{aligned}`

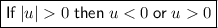
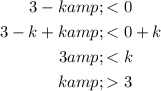
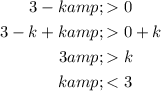
Therefore, the solution is:

`\large\boxed{\boxed{k < 3\;\;\textsf{or}\;\;k > 3}}`

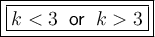
To graph the solution on a number line, place an open circle at k = 3 (since the inequality is not true at k = 3) and shade the number line to the left (for k < 3) and to the right (for k > 3) of that point.

To graph the solution on a coordinate plane, draw a vertical dashed line at x = 3 and shade each side.