Answer: non-proportional
Explanation:
To determine if a relationship is proportional or non-proportional, you can look at the ratio of
 for each pair of
for each pair of
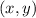 coordinates. If the ratio is constant across all pairs, then the relationship is proportional. If the ratio varies, then the relationship is non-proportional.
coordinates. If the ratio is constant across all pairs, then the relationship is proportional. If the ratio varies, then the relationship is non-proportional.
Let's calculate the
 ratio for each pair:
ratio for each pair:
1.
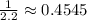
2.
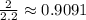
3.
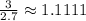
4.
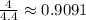
5.
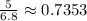
6.
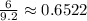
7.
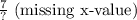
8.

9.
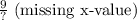
10.
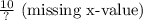
As you can see, the
 ratio is not constant across the given pairs. Therefore, the relationship is non-proportional.
ratio is not constant across the given pairs. Therefore, the relationship is non-proportional.