Final answer:
The probability that a customer has to wait more than 15 minutes is calculated using the exponential distribution formula with a service rate of 20 customers per hour. The result is approximately 0.0067, closest to option A - 0.006.
Step-by-step explanation:
To calculate the probability that a customer has to wait more than 15 minutes, we need to understand the arrival rate and service rate. Given that customers arrive at the rate of 14 per hour, we can find the average time between arrivals:
Calculation of Time Between Arrivals
Since customers arrive at a rate of 14 per hour, on average, one customer arrives every 4.29 minutes (60 / 14).
Service Rate
It is mentioned that selling tickets and providing information takes an average of 3 minutes per customer, so the service rate is 20 customers per hour (60 / 3).
Exponential Distribution
The question also states that the service times vary exponentially. Because we know the service rate is 20 per hour, the probability that a service time exceeds 15 minutes is found using the exponential distribution formula:
 , where λ is the service rate and T is the service time.
, where λ is the service rate and T is the service time.
For a service rate of 20 per hour and T = 15 minutes (or 0.25 hours), this becomes:
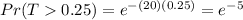 approximately equals to 0.0067, which is not given exactly in the options, but closest to option A - 0.006.
approximately equals to 0.0067, which is not given exactly in the options, but closest to option A - 0.006.
Answer Selection
The correct answer to the probability that a customer has to wait more than 15 minutes is option A, which is approximately 0.006.