Question

Point C is on line segment BD. Given CD = x, BC = 5x -5, and BD = 2x + 7,

determine the numerical length of CD.

Answer 1

3 units

Explanation:

Definition:

A line segment is a part of a line that has two endpoints. The length of a line segment is the distance between its two endpoints.

Solution:

Since point C is on line segment BD, we know that the total length of BD is equal to the sum of the lengths of BC and CD:

`\sf BD = BC + CD`

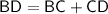
We are given that BD = 2x + 7, BC = 5x -5, and CD = x.

Substituting these values into the equation above, we get:

`\sf 2x + 7 = (5x - 5) + x`

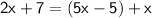
Combining like terms, we get:

`\sf 2x + 7 = 6x - 5`

Subtracting 2x from both sides, we get:

`\sf 2x + 7-2x = 6x - 5-2x`

`\sf 7 = 4x - 5`

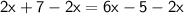
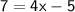
Adding 5 to both sides, we get:

`\sf 7+5 = 4x - 5+5`

`\sf 12 = 4x`

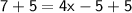
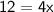
Dividing both sides by 4, we get:

`\sf (12)/(4) = (4x)/(4)`

`\sf x = 3`

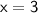
Therefore, the numerical length of the CD is 3 units.

Answer 2

CD = 3 units

Explanation:

given that point C is on line segment BD , then

BC + CD = BD ( substitute values )

5x - 5 + x = 2x + 7 ( simplify left side )

6x - 5 = 2x + 7 ( subtract 2x from both sides )

6x - 2x - 5 = 2x - 2x + 7 ( simplify both sides )

4x - 5 = 7 ( add 5 to both sides )

4x - 5 + 5 = 7 + 5 ( simplify both sides )

4x = 12 ( divide both sides by 4 )

`(4)/(4)` x =
`(12)/(4)` , that is

x = 3

Then

CD = x = 3 units