Question

Find the volume of a cube whose diagonal measures 36√3 cm.

Answer 1

`46656 cm^3`

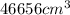
Explanation:

If a cubes diagonal measures you can solve for its sidelength by creating a triangle. Visualize the diagonal as the hypotenuse of our triangle inside the cube. Then, one of the legs would be the side of the cube itself, and the other leg would be the diagonal of the bottom side of the cube. Knowing this is a cube, we can call each side s. If each side is s, then the diagonal of the bottom face is
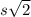`s√(2)`( this is a special triangle property,
`45-45-90` triangle.) Then we know our triangle is a right triangle, so we can use the Pythagorean theorem to solve for s.

`s^(2) + (s√(2) )^(2) = (36√(3))^2`

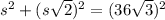
Solve this equation for s.

`s^(2) + 2s^(2) = 3888`

`3s^(2) = 3888`

`s^(2) = 1296`

`s = 36`

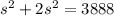
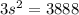
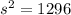
Since we now found the side length of the cube, we can find its volume by cubing the side length:

`s^3 = (36)^3 = 46656`
`cm^3`