Question

Evaluate 243^7/10 × 243^1/10.

Answer 1

The evaluation of
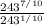`(243^(7 / 10))/(243^(1 / 10))` is 63.

To evaluate the expression
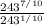`(243^(7 / 10))/(243^(1 / 10))` , you can use the properties of exponents. When you divide two terms with the same base, you subtract the exponents:

`(a^m)/(a^n)=a^(m-n)`

In this case, a=243, m=7/10, n=1/10.

`(243^(7 / 10))/(243^(1 / 10))=243^((7 / 10-1 / 10))`

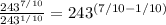
Simplifying the exponents, you can get:

`243^((7 / 10-1 / 10))=243^(6 / 10)`

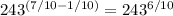
Now, reducing the fraction, you can get the equation as follows:

`243^(6 / 10)=243^(3 / 5)`

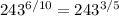
To get the required answer, you need to further simplify the RHS of the above equation. It can be done by first getting the cube value of of 243. Then, getting 1/5th of this value.

Evaluate
`243^3` :

`243^3=14348907`

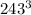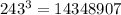
Now, take the fifth root of 14348907 (5th root is equivalent to 1/5th):

`\sqrt[5]{14348907} \approx 63`

Therefore,
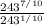`(243^(7 / 10))/(243^(1 / 10))` is approximately 63.