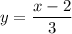Answer:
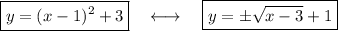
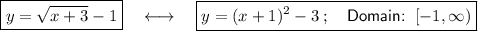


Explanation:
To find the inverse of a function, interchange the x and y variables in the original function equation and solve for y.
As the domain of the inverse function corresponds to the range of the original function, and the range of the inverse function corresponds to the domain of the original function, we also need to determine each function's range before calculating its inverse.

Question 1
Given equation:
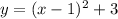
As (x - 1)² ≥ 0, the range of the function is [3, ∞).
Since the range of the function is the domain of the inverse function, the domain of the inverse function is [3, ∞).
Swap the x and y variables:

Rearrange to isolate y:
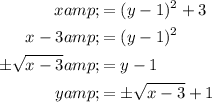
Therefore, the inverse function is:
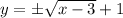

Question 2
Given equation:

As the function is only defined when the expression under the square root sign is non-negative, the range of the function is [-1, ∞).
Since the range of the function is the domain of the inverse function, the domain of the inverse function is [-1, ∞).
Swap the x and y variables:

Rearrange to isolate y:
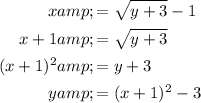
Therefore, the inverse function is:
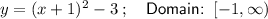

Question 3
Given equation:

The range of the function is unrestricted.
Since the range of the function is the domain of the inverse function, the domain of the inverse function is (-∞, ∞).
Swap the x and y variables:
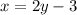
Rearrange to isolate y:
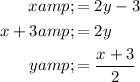
Therefore, the inverse function is:


Question 4
Given equation:
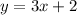
The range of the function is unrestricted.
Since the range of the function is the domain of the inverse function, the domain of the inverse function is (-∞, ∞).
Swap the x and y variables:
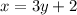
Rearrange to isolate y:
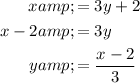
Therefore, the inverse function is: