Question

a rectangular hole is to be cut in a wall for a vent. if the perimeter of the hole is 48 in. and the length of the diagonal is a minimum, what are the dimensions of the hole?​

Answer 1

12 inches by 12 inches

Explanation:

Let the dimensions of the rectangle be l (length) and w (width).

The perimeter of a rectangle is the sum of all its sides.

So the perimeter of the rectangular hole is given by:

P = l + w + l + w

P = 2l + 2w

We are given that P = 48 inches.

48 inches = 2l + 2w

24 inches = l + w

We are also given that the length of the diagonal of the rectangle is a minimum.

The diagonal of a rectangle is given by:

`\sf d = √(l^2+ w^2)`

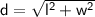
We can use the Pythagorean theorem to derive a relationship between l, w and d.

d² = l² + w²

We want to minimize d. To do that, we can make l and w as close to each other as possible. This means that the rectangle should be approximately a square.

Let's assume that l = w = a.

The perimeter of the rectangle would then be given by:

P = 2a + 2a

P = 4a

We are given that P = 48 inches.

48 inches = 4a

`\sf a = (48)/(4) inches`

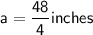
a = 12 inches

Therefore, the dimensions of the hole are 12 inches by 12 inches.