Question

Why can't 15√26 be simplified?

I'm currently learning about surds, but I don't understand this because if 10√75 -> 10√(25x3) which simplifies to 50√3, then why can't I do 15√(4x6) which I thought simplified to 2x15 = 30√6
I asked the AI and it said that I was correct, but when I searched online, I was not, can someone explain?

Answer 1

You're wrong !

• 15√26 ≠ 15√(4x6) because 4x6 = 24 and not 26.
• 15√26 is the simplest form because when we factorise √26 ,we get √(2x13) and both of these numbers can't be factorise further,thus the simplest form of 15√26 would be 15√26 itself.

`\: \\`

Answer 2

15√26 cannot be simplified further.

Explanation:

A perfect square is a whole number that can be expressed as the square of another whole number. For example, 4, 9, 16, and 25 are perfect squares because they are the squares of 2, 3, 4, and 5.

To simplify a surd, we need to identify any perfect square factors of the number under the square root sign, and take the square root of those factors.

The factors of 26 are 1, 2, 13 and 26. As none of these factors are perfect squares, this means that √26 cannot be simplified further. Therefore, 15√26 cannot be simplified further.

The factors of 75 are 1, 3, 5, 15, 25 and 75. Therefore, as one of the factors of 75 is a perfect square (25 = 5²), this means that 10√75 can be simplified further. To simplify, rewrite 75 as 25 × 3:

`10√(75)=10√(25 * 3)`

`\textsf{Apply the radical rule:} \quad √(a* b)=\sqrt{\vphantom{b}a}√(b)`

`=10√(25){√(3)`

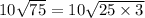
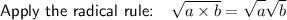
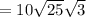
Rewrite 25 as the square of 5:

`=10√(5^2){√(3)`

`\textsf{Apply the radical rule:} \quad √(a^2)=a, \quad a \geq 0`

`\begin{aligned}&=10* 5{√(3)\\&=50√(3)\end{aligned}`

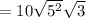
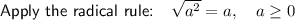
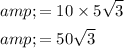
This cannot be simplified any further as none of the factors of 3 are perfect squares (3 is a prime number).