Answer: a) 1.57 seconds b) 13.5m c)17.63 m/s
Explanation: Solving for his ending position, which we are setting as x=0, or when the boy hits the water.
x =x0 +v0t+1/2 at^2
We will begin by solving in the y direction, ignoring his beginning velocity in the x direction. His initial y velocity will be 0, and his acceleration will be gravity, -9.81 m/s^2
His initial x value will be 12 m
0 = 12m + 0 m/s*t+1/2 * -9/81m/s^2 *t^2
0 = 12m + -4.905m/s^2 * t^2
moving the 12 over and then flipping signs gives us
12m = 4.905m/s^2 * t^2
dividing the height by the acceleration gives us
2.45s^2 = t^2
square rooting this gives us our answer for b, which would be
1.57 seconds
For the second part, we know that he will fly through the air for the time we just found, and he will do so in the y direction at a speed of 8.6m/s
x =x0 +v0t+1/2 at^2
x = 0 +8.6m/s * 1.57s + 1/2 * 0m/s^2 *1.57s^2
x = 13.5 m
For the third part we will use the equation v = v0 +at
for the y direction
vy = 0 + -9.81m/s^2 * 1.57s
vy = -15.386 m/s
for the x direction
vx = 8.6 + 0 *1.57s
vx = 8.6 m/s
Then you will put them together using |vtotal| =
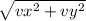
giving us the answer 17.63 m/s
drawing this is simply putting the vx and vy on arrows pointing in the proper direction