Question

Given f(x) = x^2 -12x + 27, find all values of x for which f(x) >= 7.

Answer 1

x ≤ 2, x ≥ 10

Explanation:

We are trying to find the x-values (inputs) for which the output of the function
`f(x) = x^2 - 12x + 27` is greater than or equal to 7.

One way to do this is to declare a new function, which we can call
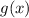`g(x)`, that is translated (shifted) down 7 units, and create a sign chart for it to find when the translated function's output is positive or zero. This will correlate to when the original function is greater than or equal to 7:

`\text{let } g(x) = f(x) - 7`

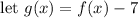
↓ plugging in
`f(x)`'s definition

`g(x) = (x^2 - 12x + 27) - 7`

↓ combining like terms

`g(x) = x^2 - 12x + 20`

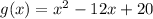
↓ factoring

`g(x) = (x-10)(x-2)`

Now, we can create a sign chart with a number line for each factor. (See the attached image.) We can solve for the following zeros:

• for
  `x-10=0`,
  `x = 10`
• for
  `x-2=0`,
  `x=2`

From the sign chart, we can identify that
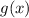`g(x)` is positive or zero over the input ranges:

x ≤ 2, x ≥ 10

Therefore, these are also the x-values for which the original function
`f(x)` will have an output greater than or equal to 7.