Question

What are the x intercepts of the function f (x) = -2x^2-3x+20

Answer 1

Explanation:

Where teh function = 0 are the x-axis intercepts

-2x^2 -3x+20 = 0

( 2x-5 )( -x -4 ) = 0 shows when x = 2.5 or -4 as x intercepts

Answer 2

2.5 and -4

Explanation:

The x-intercepts of the function f(x) = -2x^2-3x+20 are the values of x for which the function equals 0.

To find the x-intercepts, we can set the function equal to 0 and solve the resulting equation:

`\sf -2x^2-3x+20 = 0`

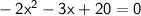
We can factor the quadratic equation as follows:

The quadratic formula is:

`\sf x = (-b \pm √(b^2 - 4ac))/(2a)`

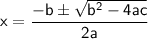
In this equation, a = -2, b = -3, and c = 20.

Substitute these values into the formula:

`\sf x = (-(-3) \pm √((-3)^2 - 4(-2)(20)))/(2(-2))`

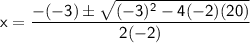
Simplify this:

`\sf x = (3 \pm √(9 + 160))/(-4)`

`\sf x = (3 \pm √(169))/(-4)`

Now, take the square root of 169:

`\sf x = (3 \pm 13)/(-4)`

Now, we have two possible solutions for x.

Either

`\sf x = (3 + 13)/(-4) = (16)/(-4) = -4`

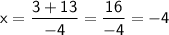
or

`\sf x = (3 - 13)/(-4) = (-10)/(-4) (5)/(2) = 2.5`

Therefore, the x-intercepts of the function are 2.5 and -4.