Question

Please help me!! this is my last question

Answer 1

let's firstly find the EQUALITY equation for the line, so hmmm to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below.

`(\stackrel{x_1}{0}~,~\stackrel{y_1}{-5})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{-3}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-3}-\stackrel{y1}{(-5)}}}{\underset{\textit{\large run}} {\underset{x_2}{1}-\underset{x_1}{0}}} \implies \cfrac{ -3 +5 }{ 1 } \implies \cfrac{ 2 }{ 1 } \implies 2`

`\begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-5)}=\stackrel{m}{2}(x-\stackrel{x_1}{0}) \implies y +5 = 2 ( x -0) \\\\\\ y+5=2x\implies \boxed{y=2x-5}`

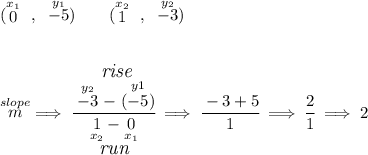
so now, let's get the INEQUALITY for it, cheap answer, the shading is above, so that means " > ", and since the line is a solid line, that means the inequality includes all values in the borderline so that means " ⩾ ".

the not so cheap answer, we can pick a point in the shaded region and do a true/false check, hmmm let's see the point (-1 , 1) is in the shaded region, that means that when x = -1, y = 1, so let's plug that in the equation

y ⩾ 2x - 5

1 ⩾ 2(-1) -5

1 ⩾ -7 ??? is that true? yeap, is true

that means that the point (-1 , 1) is on the TRUE region, so that'd be the shaded area.

y ⩾ 2x - 5