Answer:
Step-by-step explanation:
The discrepancy between the calculated maximum possible speed of the miner and the actual speed observed at the bottom of the slide can be explained by several factors:
- Friction: Even though the wooden slides are smooth, there's still some degree of friction between the miner's clothing or equipment and the slide. This friction acts against the motion, slowing the miner down as they descend.
- Air Resistance: As the miner moves down the slide, they'll encounter air resistance, which increases with their speed. This resistance can play a significant role in reducing their final velocity
When analysing the motion of the miner on the slide, the primary principle at play is the conservation of energy. In an ideal situation without any external forces, the potential energy the miner has at the top of the slide is converted entirely into kinetic energy at the bottom:
![\[ PE_{\text{top}} = KE_{\text{bottom}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/w9g8f5mtc74z29q5luqs1ci14ea90wue66.png)
For potential energy
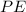 due to height
due to height
 and mass
and mass
 :
:
![\[ PE = mgh \]](https://img.qammunity.org/2024/formulas/physics/high-school/hihu6zeucez3bf4r8udgxhwanpcnbf1dir.png)
Where:
-
 is the acceleration due to gravity (approx.
is the acceleration due to gravity (approx.
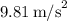 ).
).
For kinetic energy
 for a velocity
for a velocity
 :
:
![\[ KE = (1)/(2)mv^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/vff65mwlyttobps790tmf5z1vevvg1n24b.png)
Equating the two energies:
![\[ mgh = (1)/(2)mv^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/8jp0c289fwzzyl4pqrnocketdpk75zw8sw.png)
From this, we can derive the theoretical maximum speed
 at the bottom:
at the bottom:
![\[ v = √(2gh) \]](https://img.qammunity.org/2024/formulas/physics/high-school/utrb5773abfhh03l0f7oyvm5cdvk85tzik.png)
However, the observed speed is less than this value, which brings us to the reason: friction.
The work done against friction is given by:
![\[ W = f * d \]](https://img.qammunity.org/2024/formulas/physics/high-school/4v6an1uge2nkkzcoz67q10lvd8f8rqx7ws.png)
Where
 is the force of friction and
is the force of friction and
 is the distance (length of the slide). The force of friction (assuming a constant coefficient of friction
is the distance (length of the slide). The force of friction (assuming a constant coefficient of friction
 ) is:
) is:
![\[ f = \mu * N \]](https://img.qammunity.org/2024/formulas/physics/high-school/fokeimo7ejdmbq00m06eubwi734twzdnzo.png)
Where
 is the normal (or perpendicular) force. For an inclined plane,
is the normal (or perpendicular) force. For an inclined plane,
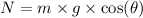 , where
, where
 is the angle of the slide with respect to the horizontal.
is the angle of the slide with respect to the horizontal.
Considering the work-energy theorem, the work done against friction reduces the kinetic energy of the miner:
![\[ (1)/(2)mv^2 = mgh - \mu * m * g * \cos(\theta) * d \]](https://img.qammunity.org/2024/formulas/physics/high-school/qc1h8s3lf9mfcvd7bdwir7s09lwh6ic7t1.png)
From this, you can derive the actual speed at the bottom considering friction. This speed will be less than the
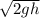 derived earlier because of the energy lost to overcome the friction.
derived earlier because of the energy lost to overcome the friction.
Air resistance (or drag) for objects moving through the air is given by:
![\[ F_{\text{drag}} = (1)/(2) * \rho * v^2 * A * C_d \]](https://img.qammunity.org/2024/formulas/physics/high-school/l3jpkhi8g542em25agqjx6r15yiw53uhym.png)
Where:
-
 is the air density (about
is the air density (about
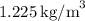 at sea level).
at sea level).
-
 is the velocity of the miner.
is the velocity of the miner.
-
 is the cross-sectional area of the miner facing the direction of motion.
is the cross-sectional area of the miner facing the direction of motion.
-
 is the drag coefficient, which depends on the shape of the object (for a human, this could be around 1.0-1.3 when facing the air, but this varies greatly).
is the drag coefficient, which depends on the shape of the object (for a human, this could be around 1.0-1.3 when facing the air, but this varies greatly).
The kinetic energy at the bottom, in the presence of both friction and air resistance, will be:
![\[ (1)/(2)mv^2 = mgh - \mu * m * g * \cos(\theta) * d - \int F_{\text{drag}} \, ds \]](https://img.qammunity.org/2024/formulas/physics/high-school/sy5shtj9gppst5pu96udiw9ggeqsxefzoo.png)
Where
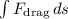 represents the work done against air resistance over the distance of the slide.
represents the work done against air resistance over the distance of the slide.