Question

Identify the original function and x value of the instantaneous rate of change. lim ((3x-9x^2) + (42))/(x+2) x->2

Answer 1

Explanation:

Given:

`\[ \text{lim}_(x \to 2) ((3x - 9x^2) + 42)/(x + 2) \]`

The standard form of the difference quotient for a function
`\( f(x) \)` at a point
`\( x \)` is:

`\[ f'(x) = \text{lim}_(h \to 0) (f(x+h) - f(x))/(h) \]`

Comparing this to the given expression, we can infer that the function is being evaluated at
`\( x \)` and
`\( x + 2 \)` (or
`\( x + h \)` where
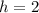`\( h = 2 \)`). This is not the standard difference quotient, but we can still determine the original function by recognizing the numerator of the quotient.

The original function seems to be:

`\[ f(x) = 3x - 9x^2 + 42 \]`

Given the limit is as
`\( x \to 2 \)`, the
`\( x \)`-value at which the instantaneous rate of change is being evaluated is:

`\[ x = 2 \]`

Thus, the original function is
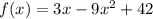`\( f(x) = 3x - 9x^2 + 42 \)` and the
`\( x \)`-value is 2.