Question

A motor car of mass 20 quintals is moving with a velocity of 60 km per hour. By the application of brakes, it is brought to rest in a distance of 3 kilometers. Find the average force of resistance in newtons.

Answer 1

Approximately
`92.6\; {\rm N}` opposite to the initial direction of motion, assuming that the surface is level and that mass of the vehicle is
`2000\; {\rm kg}`.

Step-by-step explanation:

Forces on this vehicle include weight (downward), normal force (upward), and resistance (backward.) Under the assumptions that the surface is level, the only unbalanced force on this vehicle would be resistance. Hence, the force of resistance on this vehicle would have the same value as the net force.

The average value of this net force can be found in the following steps:

• Find average acceleration of the vehicle using SUVAT equations.
• Find average net force on this vehicle from average acceleration using Newton's Laws of Motion.

Let the initial direction of motion be the positive direction. Initial velocity and displacement are both in that direction and would both be positive. Make sure all quantities are measured in standard units:

• Mass:
  `m = 2000\; {\rm kg}`.
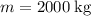• Initial velocity:
  
  `\begin{aligned} u &= (60\; {\rm km\cdot h^(-1)}) * \frac{1\; {\rm h}}{3600\; {\rm s}} * \frac{1000\; {\rm m}}{1\; {\rm km}} \\ &= (50)/(3)\; {\rm m\cdot s^(-1)}\end{aligned}`.
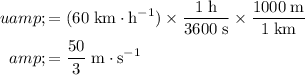• Displacement:
  `x = 3000\; {\rm m}`.

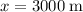The SUVAT equation
`v^(2) - u^(2) = 2\, a\, x` provides a relationship between initial velocity
`u`, final velocity
`v`, displacement
`x`, and acceleration
`a`. In this question:

• Initial velocity is
  `u = (50/3)\; {\rm m\cdot s^(-1)}`.
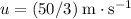• Final velocity is
  `v = 0\; {\rm m\cdot s^(-1)}` since the vehicle has completely stopped.
• Displacement is
  `x = 3000\; {\rm m}`.

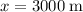Rearrange this equation to find average acceleration
`a`:

`\begin{aligned}a &= (v^(2) - u^(2))/(2\, x) \\ &= (0^(2) - (50/3)^(2))/(2\, (3000))\; {\rm m\cdot s^(-2)} \\ &= \left(-(5)/(108)\right)\; {\rm m\cdot s^(-2)}\end{aligned}`.

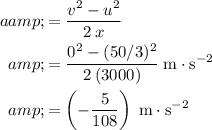Note that acceleration is negative because the direction of acceleration is opposite to the original direction of motion, which is the positive direction.

By Newton's Laws of Motion, the net force on this vehicle would be equal to the product of mass and acceleration:

`\begin{aligned}(\text{net force}) &= (\text{mass})\, (\text{acceleration}) \\ &= (2000\; {\rm kg})\, \left(\left(-(5)/(108)\right)\; {\rm m\cdot s^(-2)}\right) \\ &\approx (-92.6)\; {\rm N}\end{aligned}`.

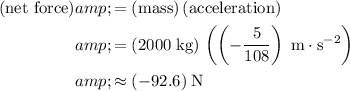Similarly, average net force on this vehicle is negative because the direction of net force is opposite to the positive direction.

Under the assumptions, the force of resistance on the vehicle would have the same value as net force. Hence, the average force of resistance on this vehicle would be approximately
`92.6\; {\rm N}` opposite to the original direction of motion.