Find the difference quotient for f(x)=8-x^(2) please show work

Question

Find the difference quotient for
`f(x)=8-x^(2)`

please show work

Answer 1

`- 2x -h`

Explanation:

The difference quotient is used to estimate the derivative of a function at a specific point. It measures the average rate of change of the function over a small interval around the given point.

The point (x + h, f(x + h)) is a small distance along the curve from (x, f(x)). As h gets smaller, the distance between the two points gets smaller. The closer the points, the closer the line joining them will be to the tangent line at that point.

The difference quotient of a function y = f(x) is defined as:

`(f(x + h) - f(x))/(h)`

To find the difference quotient for (f(x) = 8 - x², begin by substituting f(x + h) and f(x) into the formula:

`((8 - (x + h)^2) - (8 - x^2))/(h)`

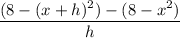
Expand the expressions inside the brackets:

`(8 - (x^2 + 2hx + h^2) - 8 + x^2)/(h)`

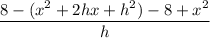
Simplify the numerator:

`(8 - x^2 - 2hx -h^2 - 8 + x^2)/(h)`

`(- 2hx -h^2)/(h)`

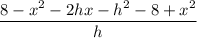
Cancel out h from the numerator and denominator:

`- 2x -h`

Therefore, the difference quotient for the function f(x) = 8 - x² is:

`\Large\boxed{\boxed{- 2x -h}}`