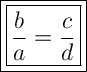Question

Perpenticular lines, image below.

Answer 1

`\textsf{B)} \quad (b)/(a)=(c)/(d)`

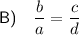
Explanation:

Parallel lines have the same slope. Therefore, an equation that can be used to prove that two lines are parallel is one where their slopes are equal.

The formula for the slope of a line is:

`\boxed{\begin{minipage}{8cm}\underline{Slope Formula}\\\\Slope $(m)=(y_2-y_1)/(x_2-x_1)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are two points on the line.\\\end{minipage}}`

From observation of the given diagram, two points on the first line are:

• (x₁, y₁) = (-a, 0)
• (x₂, y₂) = (0, b)

Substitute the points into the slope formula to find the slope of the line:

`m=(b-0)/(0-(-a))=(b)/(a)`

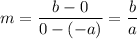
From observation of the given diagram, two points on the second line are:

• (x₁, y₁) = (0, -c)
• (x₂, y₂) = (d, 0)

Substitute the points into the slope formula to find the slope of the line:

`m=(0-(-c))/(d-0)=(c)/(d)`

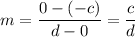
Equate the two slopes:

`(b)/(a)=(c)/(d)`

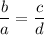
Therefore, the equation that could prove that the two lines are parallel is:

`\Large\boxed{\boxed{(b)/(a)=(c)/(d)}}`