This question I am stuck on

Question

asked Jun 13, 2024 76.8k views

1 Answer

Nagesh · Answer 1 · 2024-06-17T06:16:17+0000

Hello!

Answer:

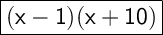
$\Large \boxed{\sf (x-1)(x+10)}$
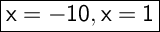
$\Large \boxed{\sf x = -10,x =1}$

Explanation:

a) We want to factorize this expression:

$\sf x^2 + 9x-10$

→ Factorize the expression:

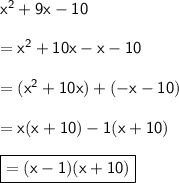
$\sf x^2 + 9x-10\\\\= x^2 + 10x-x-10\\\\= (x^2 +10x)+(-x-10)\\\\= x(x+10) - 1(x+10)\\\\\boxed{\sf = (x-1)(x+10)}$

b) We want to solve this equation:

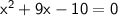
$\sf x^2 + 9x-10 = 0$

→ Before, we factored the left hand side, so the equation is equal to:

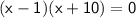
$\sf (x-1)(x+10) = 0$

→ So we have two equations, the solutions of these equations are the solutions of our equation x² + 9x - 10 = 0.

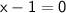
$\sf x-1=0$

$\sf x+10 = 0$

→ Let's solve these equations:

◼ Add 1 to both sides:

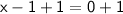
$\sf x-1+1=0+1$

◼ Simplify both sides:

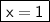
$\boxed{\sf x=1}$

◼ Subtract 10 from both sides:

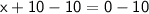
$\sf x+10-10 = 0-10$

◼ Simplify both sides:

$\boxed{\sf x=-10}$

Conclusion:

The expression x² + 9x - 10 is equal to (x - 1)(x + 10).

The solutions of the equation x² + 9x - 10 = 0 are -10 and 1.