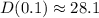Question

Because of the curvature of the earth, the maximum distance D that you can see from the top of a tall building or from an airplane at height h is given by the function D(h) =√(2rh + h²) where r = 3960 mi is the radius of the earth and D and h are measured in miles. (Assume there are 5280 feet in a mile. Round your answers to one decimal place.) How far can you see from the observation deck of Toronto's CN Tower, 1135 ft above the ground? _____ mi

Answer 1

From the observation deck of the CN Tower, 1135 feet above the ground, one can see approximately 41.3 miles to the horizon after converting the height into miles and applying the distance function.

Step-by-step explanation:

The maximum distance D that one can see from a height h above the Earth's surface is given by the function D(h) = √(2rh + h²), where r is the radius of the Earth. For the CN Tower with an observation deck at 1135 feet above the ground, we first need to convert this height into miles by dividing by the number of feet in a mile. Therefore, h = 1135 feet / 5280 feet/mile = 0.215 miles approximately. We can then calculate D by substituting h into the function:

D(h) = √(2 * 3960 miles * 0.215 miles + (0.215 miles)²) = √(2 * 3960 * 0.215 + 0.215²) = √(1701.6 + 0.0462) = √1701.6462 ≈ 41.3 miles

Therefore, from the observation deck of the CN Tower, you can see approximately 41.3 miles to the horizon.

Answer 2

`\(D(0.1) \approx 28.1\)` miles and
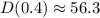`\(D(0.4) \approx 56.3\)` miles

How to find ind D(0.1) and D(0.4)?

To find
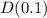`\(D(0.1)\)` and
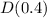`\(D(0.4)\)` using the given formula
`D(h) = √(2rh+h^2 )` when
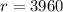`\(r = 3960\)` miles (D, h, r all in miles)

For
`\(D(0.1)\)`:

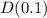`\[D(0.1) = √(7920(0.1) + (0.1)^2) = √(792 + 0.01) = √(792.01) = 28.143 \approx 28.1 \text{ miles}\]`

For
`\(D(0.4)\)`:

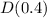`\[D(0.4) = √(7920(0.4) + (0.4)^2) = √(3168 + 0.16) = √(3168.16) = 56.286 \approx 56.3 \text{ miles}\]`

Therefore,
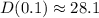`\(D(0.1) \approx 28.1\)` miles and
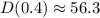`\(D(0.4) \approx 56.3\)` miles.

Distance refers to a quantified representation of the spatial separation or extent between two distinct points or entities. It encapsulates the amount of space existing between these points or signifies the length of the route traversed between them.

In physics and mathematics, distance finds measurement in diverse units like meters, kilometers, miles, feet, among others, depending on the specific context or scale of measurement employed.

See missing part of the question on the attached image.