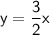Question

Write an equation of a line and interpret the slope (image below)

Answer 1

`\sf y = (3)/(2)x`

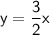
Step-by-step explanation:

Given:

• Rise = 6
• Run = 4
• Passes through the origin
• x axis is age in years
• y axis is the height of tree in feet

To find:

• Equation of the line

Solution:

Since we have the rise and run, we know that the line passes through the origin (0,0).

With this information, we can find the equation of the line using the slope-intercept form, which is:

`\sf y = mx+ c`

Where:

- "y" is the value on the y-axis (height of the tree).

- "x" is the value on the x-axis (age in years).

- "m" is the slope of the line.

- "c" is the constant term.

In this case, the rise is 6 and the run is 4, so we can calculate the slope (m) as:

`\sf = \frac{\text{Rise}}{\text{Run}} = (6)/(4) = (3)/(2)`

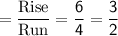
To find constant, substitute the value x and y in the slope intercept form, we get

`\sf 0* y = 0* x = c`

c = 0

Now that we have the slope and constant, we can write the equation of the line as:

`\sf y = (3)/(2)x+0`

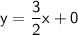
So, the equation of the line that represents the height of the tree (y) in terms of age in years (x) is:

`\sf y = (3)/(2)x`

Answer 2

slope = 3/2

The tree grows 3 ft every 2 yrs.

Step-by-step explanation:

We can find the slope of the line using the formula:

slope = rise / run

↓ plugging in the given values

slope = 6 / 4

↓ simplifying the fraction

slope = 3/2

In this context, y represents a tree's height over x amount of years.

So, we can say that the tree represented by the line grows 3 ft every 2 yrs.