Question

A population of insects increases at a rate 300+10t+0.3t2 insects per day ( t in days). Find the insects population after 5 days assuming that there are 40 insects at t=0. (Give your answer as a whole or exact number.)

Answer 1

The insect population after 5 days, as a whole number, would be 1677.5 insects.

Given the rate of increase function for the population of insects: 300 + 10t + 0.3t² insects per day, where t is in days.

To find the population after 5 days, we'll integrate this function and add the initial population of 40 insects at t = 0.

First, integrate the rate of increase function with respect to time t:

`\(\int (300 + 10t + 0.3t^2) \, dt\)`

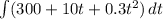
The integral of 300 with respect to t is 300t.

The integral of 10t with respect to t is
`\((10)/(2)t^2 = 5t^2\)`.

The integral of 0.3t² with respect to t is
`\((0.3)/(3)t^3 = 0.1t^3\)`.

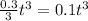Now, let's evaluate the definite integral from 0 to 5 (as we're looking for the population after 5 days):

Population after t days = 300t + 5t² + 0.1t³ + C, where C is the constant of integration.

Given the initial population is 40 insects at t=0, substitute t = 0 into the equation:

40 = 300(0) + 5(0)² + 0.1(0)³ + C

40 = 0 + 0 + 0 + C

C = 40

So, the equation becomes:

Population after t days = 300t + 5t² + 0.1t³ + 40

Now, calculate the population after 5 days (t = 5):

Population after 5 days = 300(5) + 5(5)² + 0.1(5)³ + 40

Population after 5 days = 1500 + 125 + 12.5 + 40

Population after 5 days = 1637.5 + 40

Population after 5 days = 1677.5 insects.