Answer:
A. There are 1.86 times more moles of gas A (CO) than gas B (SO2).
There are more molecules of CO than SO2
B. Container B (SO2) contains more mass.
C. Vessel B has the highest average kinetic energy of the molecules
Step-by-step explanation:
The Ideal Gas Law says:
PV = nRT, where P, V, and T are pressure, volume, and temperature (in Kelv1n). R is the gas constant and n is the moles of gas.
The volumes are the same, so lets choose 1 L as a starting point.
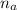 is the moles of gas in container A
is the moles of gas in container A
 is the moles of gas in container B
is the moles of gas in container B
Vessel A:
PV = nRT
(1 atm)*(1 L) =
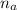 *(R)*(273K)
*(R)*(273K)
Vessel B:
PV = nRT
(0.5 atm)*(1 L) =
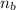 *(R)*(293K)
*(R)*(293K)
Lets rearrange both equations to isolate the moles, n, of each gas.
Vessel A:
(1 atm)*(1 L) =
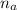 *(R)*(273K)
*(R)*(273K)
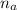 = ((1 atm)*(1 L) =)/((R)*(273K))
= ((1 atm)*(1 L) =)/((R)*(273K))
Vessel B:
(0.5 atm)*(1 L) =
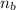 *(R)*(293K)
*(R)*(293K)
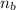 = ((0.5 atm)*(1 L))/((R)*(293K))
= ((0.5 atm)*(1 L))/((R)*(293K))
Now lets find the ratio of
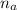 /
/
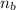
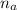 /
/
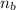 =[((1 atm)*(1 L) =)/((R)*(273K))]/[((0.5 atm)*(1 L))/((R)*(293K))])
=[((1 atm)*(1 L) =)/((R)*(273K))]/[((0.5 atm)*(1 L))/((R)*(293K))])
Rearrange and solve:
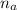 /
/
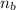 =[((1 atm)*(1 L) =)/((R)*(273K))]/[((0.5 atm)*(1 L))/((R)*(293K))])
=[((1 atm)*(1 L) =)/((R)*(273K))]/[((0.5 atm)*(1 L))/((R)*(293K))])
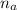 /
/
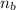 =[((1 atm)*(1 L) )/((R)*(273K))] * [((R)*(293K))/((0.5 atm)*(1 L))])
=[((1 atm)*(1 L) )/((R)*(273K))] * [((R)*(293K))/((0.5 atm)*(1 L))])
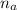 /
/
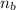 =[((1 )*(1 ) )/((273))] * [((293))/((0.5)*(1 ))])
=[((1 )*(1 ) )/((273))] * [((293))/((0.5)*(1 ))])
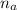 /
/
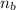 =[(1 )] * ((293/273))/((0.5)*(1 ))])
=[(1 )] * ((293/273))/((0.5)*(1 ))])
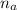 /
/
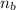 =(1)*(0.932)/(0.5)
=(1)*(0.932)/(0.5)
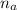 /
/
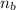 = 1.86
= 1.86
A. There are 1.86 times more moles of gas A (CO) than gas B (SO2).
There are more molecules of CO than SO2
B. Molar masses:
CO = 28 g/mole
SO2 = 64 g/mole
The ratio of molar masses, SO2/CO is (64/28) or 2.28
[1.86x moles CO)/(1x moles SO2) * (28/64) = 0.81
Container B (SO2) contains more mass.
C. Vessel B has the highest average kinetic energy of the molecules since it is at the higher temperature. (20 C vs, 0 C).