Final Answer:
The total magnetic field
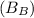 at point B created by currents
at point B created by currents
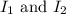 can be expressed as follows:
can be expressed as follows:
![\[ B_B = (\mu_0)/(4\pi) \left( (I_1)/(D_1) + (I_2)/(D_2) \right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/8jptk8ymc81qtbsmsabmhedw4lggeiryn8.png)
Step-by-step explanation:
The magnetic field at a point due to a current-carrying wire is given by Ampere's Law. For two parallel straight conductors carrying currents
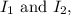 separated by distances
separated by distances
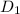 and
and
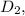 the total magnetic field at a point between them (point B) is the sum of the magnetic fields produced by each current.
the total magnetic field at a point between them (point B) is the sum of the magnetic fields produced by each current.
Ampere's Law states that the magnetic field
 around a closed loop is proportional to the total current passing through the loop. For a single straight conductor, the formula is
around a closed loop is proportional to the total current passing through the loop. For a single straight conductor, the formula is
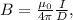 where
where
 is the permeability of free space,
is the permeability of free space,
 is the current, and
is the current, and
 is the distance from the wire.
is the distance from the wire.
In the case of two parallel conductors at different distances
 and
and
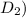 from point B, the total magnetic field (\(B_B\)) is the sum of the individual magnetic fields:
from point B, the total magnetic field (\(B_B\)) is the sum of the individual magnetic fields:
![\[ B_B = (\mu_0)/(4\pi) \left( (I_1)/(D_1) + (I_2)/(D_2) \right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/8jptk8ymc81qtbsmsabmhedw4lggeiryn8.png)
This expression accounts for the contributions of both currents
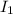 and
and
 to the magnetic field at point B.
to the magnetic field at point B.