Question

I do t know how to solve this

Answer 1

(-2, 2) and (3, 7)

Explanation:

Given system of absolute value equations:

`\begin{cases}y=|x+4|\\y=|x^2-2|\end{aligned}`

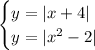
To solve this system, we can use the method of substitution.

Substitute the second equation into the first:

`|x^2-2|=|x+4|`

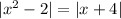
Now, set the argument of the absolute value function on the left side of the equation to both the positive and negative arguments of the absolute value function on the right side of the equation, and solve for x in both cases.

Case 1 (positive)

`\begin{aligned}x^2-2&=x+4\\x^2-x-6&=0\\x^2-3x+2x-6&=0\\x(x-3)+2(x-3)&=0\\(x+2)(x-3)&=0\\\\x+2&=0\implies x=-2\\x-3&=0\implies x=3\end{aligned}`

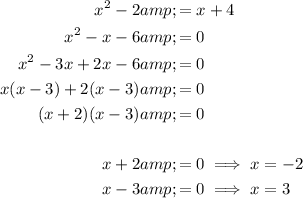
Case 2 (negative)

`\begin{aligned}x^2-2&=-(x+4)\\x^2-2&=-x-4\\x^2+x+2&=0\end{aligned}`

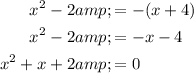
This quadratic cannot be solved by factoring, so we can use the quadratic formula to solve for x:

`x=(-b \pm √(b^2-4ac))/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

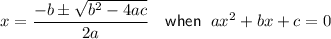
Therefore:

`x=(-1 \pm √(1^2-4(1)(2)))/(2(1))`

`x=(-1 \pm √(-7))/(2)`

`x=(-1 \pm √(7)\:i)/(2)`

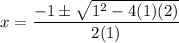
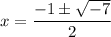
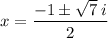
Since the solutions are complex numbers, they are not applicable.

Solution

Substitute the found values of x into one of the equations to find the corresponding values of y:

`\begin{aligned}x=-2\implies y&=|-2+4|\\y&=|2|\\y&=2\end{aligned}`

`\begin{aligned}x=3\implies y&=|3+4|\\y&=|7|\\y&=7\end{aligned}`

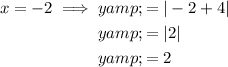
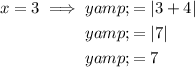
Therefore, the solutions to the given system of absolute value equations are (-2, 2) and (3, 7).