Question

A tennis ball of mass 250 g hits on a tennis bat with the velocity 5m / s . Calculate the change in momentum if the ball bounces back on the same path with the same speed .​

Answer 1

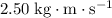`2.50\; {\rm kg\cdot m\cdot s^(-1)}` towards the direction in which the tennis ball bounced back.

Step-by-step explanation:

When an object of mass
`m` is moving at a velocity of
`\mathbf{v}`, the momentum
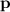`\mathbf{p}` of this object would be
`\mathbf{p} = m\, \mathbf{v}`.

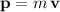Make sure mass is measured in standard units (kilograms):
`m = 250\; {\rm g} = 0.250\; {\rm kg}`.

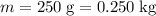Both momentum and velocity are vector quantities and are directional. The value of a vector quantity would change if direction changes, even if the magnitude of the quantity stays the same.

The speed of an object is the magnitude of its velocity. Thus, even if the speed (magnitude of velocity) of this tennis ball stays the same, velocity would change if direction of motion changes.

To find the change in momentum of this tennis ball, start by finding the value of momentum before and after the impact. Subtract the initial value of momentum from the new value to find the change.

Assume that the positive direction is the direction in which the tennis ball bounces back. Velocity and momentum would be positive if directed toward the positive direction, and negative if directed in the opposite direction.

The ball was initially moving opposite to the positive direction. Hence, the initial velocity of the ball would be negative:
`\mathbf{v}(\text{initial}) = (-5)\; {\rm m\cdot s^(-1)}`. The direction of momentum is the same as that of velocity. Thus, initial momentum of this tennis ball would be:

`\begin{aligned} \mathbf{p}(\text{initial}) &= m\, \mathbf{v}(\text{initial}) \\ &= (0.250\; {\rm kg}) \, ((-5)\; {\rm m\cdot s^(-1)}) \\ &= (-1.25)\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.
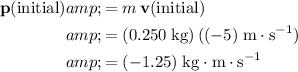When the ball bounces back, it would be moving toward the positive direction. The new velocity of the ball would be positive:
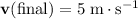`\mathbf{v}(\text{final}) = 5\; {\rm m\cdot s^(-1)}`. The new momentum of this tennis ball would be:

`\begin{aligned} \mathbf{p}(\text{final}) &= m\, \mathbf{v}(\text{final}) \\ &= (0.250\; {\rm kg}) \, (5\; {\rm m\cdot s^(-1)}) \\ &= 1.25\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

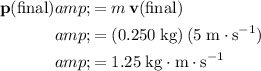Subtract the initial value of momentum from the final value to find the change:

`\begin{aligned} \Delta \mathbf{p} &= \mathbf{p}(\text{final}) - \mathbf{p}(\text{initial}) \\ &= (1.25\; {\rm kg\cdot m\cdot s^(-1)}) - ((-1.25)\; {\rm kg\cdot m\cdot s^(-1)}) \\ &= 2.50\; {\rm kg\cdot m\cdot s^(-1)}\end{aligned}`.

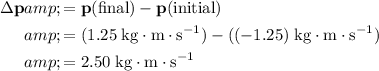In other words, the change in the momentum of this tennis ball is
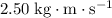`2.50\; {\rm kg\cdot m\cdot s^(-1)}`. Since this quantity is positive, it would point in the positive direction- towards the direction in which the tennis ball bounces back.