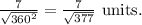Question

Find the distance between the lines 8x + 15y – 5 = 0 and 16x-30y-12=0

Answer 1

The distance between the lines
`\(8x + 15y - 5 = 0\) and \(16x - 30y - 12 = 0\) is \((7)/(√(377))\) units.`

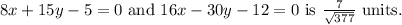
Step-by-step explanation:

To find the distance between two skew lines, we'll use the formula for the distance between a point and a line. We need to select a point on one line and then find the perpendicular distance from that point to the other line. The normal vectors to the lines will help us achieve this.

Given the equations of the lines are
`\(8x + 15y - 5 = 0\) and \(16x - 30y - 12 = 0\), these can be rewritten in slope-intercept form: \(y = -(8)/(15)x + (1)/(3)\) and \(y = (8)/(15)x + (2)/(5)\).`

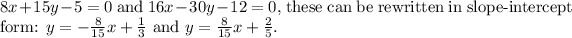
The direction vectors of these lines are
`\(\mathbf{v_1} = (15, -8)\) and \(\mathbf{v_2} = (15, 8)\). The normal vector \(n\) between these lines is obtained by taking the cross product of \(\mathbf{v_1}\) and \(\mathbf{v_2}\).`

`\(n = \mathbf{v_1} * \mathbf{v_2} = (15, -8, 0) * (15, 8, 0) = (0, 0, 360)\).`

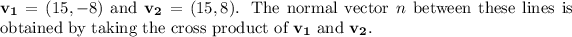
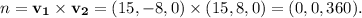
The magnitude of the normal vector
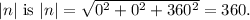`\(|n|\) is \(|n| = √(0^2 + 0^2 + 360^2) = 360\).`To find the distance \(d\) between the lines, divide the absolute value of the constant term in one of the line equations by the magnitude of the normal vector:
`\(d = (|-5 - (-12)|)/(|n|) = (7)/(360)\).`

Therefore, the distance between the lines is
`\((7)/(√(360^2)) = (7)/(√(377))\) units.`