Evaluate the derivatives of the function. Do NOT simplify your answer. Please show me how to do this step by step. y=arcsin(cosx)+arcsin(2x)

Question

Evaluate the derivatives of the function. Do NOT simplify your answer. Please show me how to do this step by step.


`y=arcsin(cosx)+arcsin(2x)`

Answer 1

`f'(x)=-(\sin x)/(√(1-\cos^2x))+(2)/(√(1-4x^2))`

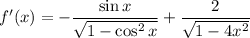
Explanation:

Given function:

`y=\arcsin(\cos x)+\arcsin(2x)`

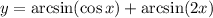
To differentiate the given function, we can use the sum rule for differentiation which states that the derivative of a sum of functions is the sum of the derivatives of those functions.

First term

Differentiate the first term arcsin(cos x) using the chain rule.

`\boxed{\begin{minipage}{5.4 cm}\underline{Chain Rule for Differentiation}\\\\If $y=f(u)$ and $u=g(x)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

`\textsf{Let}\;\;y=\arcsin(u)\;\;\textsf{where}\;\;u=\cos x`

Differentiate the two parts separately:

`\frac{\text{d}y}{\text{d}u}=(1)/(√(1-u^2))`

`\frac{\text{d}u}{\text{d}x}=-\sin x`

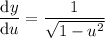
Put everything into the chain rule formula:

`\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}* \frac{\text{d}u}{\text{d}x}`

`\frac{\text{d}y}{\text{d}x}=(1)/(√(1-u^2))* (-\sin x)`

`\frac{\text{d}y}{\text{d}x}=-(\sin x)/(√(1-u^2))`

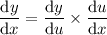
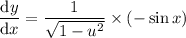
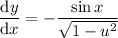
Substitute back in u = cos x:

`\frac{\text{d}y}{\text{d}x}=-(\sin x)/(√(1-\cos^2x))`

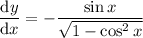
Second term

Differentiate the second term arcsin(2x) using the chain rule.

`\textsf{Let}\;\;y=\arcsin(u)\;\;\textsf{where}\;\;u=2x`

Differentiate the two parts separately:

`\frac{\text{d}y}{\text{d}u}=(1)/(√(1-u^2))`

`\frac{\text{d}u}{\text{d}x}=2`

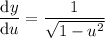
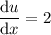
Put everything into the chain rule formula:

`\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}* \frac{\text{d}u}{\text{d}x}`

`\frac{\text{d}y}{\text{d}x}=(1)/(√(1-u^2))* 2`

`\frac{\text{d}y}{\text{d}x}=(2)/(√(1-u^2))`

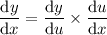
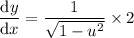
Substitute back in u = 2x:

`\frac{\text{d}y}{\text{d}x}=(2)/(√(1-(2x)^2))`

`\frac{\text{d}y}{\text{d}x}=(2)/(√(1-4x^2))`

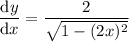
Now, we have the derivatives of both terms, and we can add them together to find the derivative of f(x):

`f'(x)=-(\sin x)/(√(1-\cos^2x))+(2)/(√(1-4x^2))`

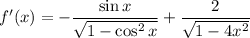
Therefore, the derivative of the given function is:

`\large\boxed{\boxed{f'(x)=-(\sin x)/(√(1-\cos^2x))+(2)/(√(1-4x^2))}}`

`\hrulefill`

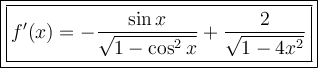
Differentiation rules used:

`\boxed{\begin{array}{l}\underline{\textsf{Differentiation Rules}}\\\\\frac{\text{d}}{\text{d}x}(\cos x)=-\sin x\\\\\frac{\text{d}}{\text{d}x}(\arcsin x)=(1)/(√(1-x^2))\\\\\frac{\text{d}}{\text{d}x}(ax)=a\\\\\end{array}}`