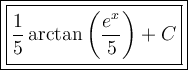Evaluate the following integrals, please show steps. \int\limits (e^x)/(e^2^x+25) dx.

Question

Evaluate the following integrals, please show steps.


`\int\limits (e^x)/(e^2^x+25) dx.`

Answer 1

`(1)/(5)\arctan \left((e^x)/(5)\right)+C`

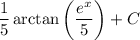
Explanation:

Given integral:

`\displaystyle \int (e^x)/(e^(2x)+25)\; \text{d}x`

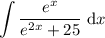
To integrate the given integral, we can use the method of substitution.

`\textsf{Let}\;\;u=e^x`

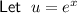
Differentiate u with respect to x:

`\frac{\text{d}u}{\text{d}x}=e^x`

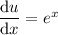
Rearrange to isolate dx:

`\text{d}x=(1)/(e^x)\;\text{d}u}`

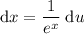
Rewrite the original integral in terms of u and du:

`\begin{aligned}\displaystyle \int (e^x)/(e^(2x)+25)\; \text{d}x&=\int (u)/(u^2+25)\cdot (1)/(e^x)\;\text{d}u}\\\\&=\int (u)/(u^2+25)\cdot (1)/(u)\;\text{d}u}\\\\&=\int (1)/(u^2+25)\;\text{d}u}\end{aligned}`

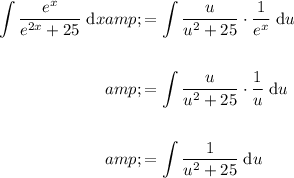
Rewrite 25 as 5²

`=\displaystyle \int (1)/(u^2+5^2)\;\text{d}u}`

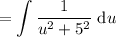
We can now use the following integration rule to evaluate the integral:

`\boxed{\displaystyle \int(1)/(a^2+x^2)\; \text{d}x=(1)/(a) \arctan \left((x)/(a)\right)+\text{C}}`

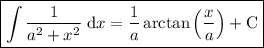
In this case, a = 5 and x = u. Therefore:

`\displaystyle \int (1)/(u^2+5^2)\;\text{d}u}=(1)/(5)\arctan \left((u)/(5)\right)+C`

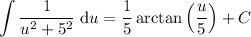
Substitute back in
`u = e^x`:

`=(1)/(5)\arctan \left((e^x)/(5)\right)+C`

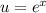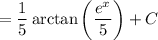
Therefore, the evaluation of the given integral is:

`\large\boxed{\boxed{(1)/(5)\arctan \left((e^x)/(5)\right)+C}}`