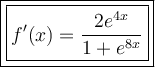Evaluate the derivatives of the function. Do NOT simplify your answer. Please show me how to do this step by step. f(x)=(1)/(2) arctan(e^4^x)

Question

Evaluate the derivatives of the function. Do NOT simplify your answer. Please show me how to do this step by step.


`f(x)=(1)/(2) arctan(e^4^x)`

Answer 1

`f'(x)=(2e^(4x))/(1+e^(8x))`

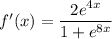
Explanation:

Given function:

`f(x)=(1)/(2)\arctan \left(e^(4x)\right)`

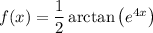
To differentiate the given function, we can use the chain rule.

`\boxed{\begin{minipage}{5.4 cm}\underline{Chain Rule for Differentiation}\\\\If $y=f(u)$ and $u=g(x)$ then:\\\\$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}$\\\end{minipage}}`

`\textsf{Let}\;\;y=(1)/(2)\arctan(u)\;\;\textsf{where}\;\;u=e^(4x)`

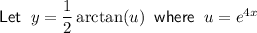
Differentiate the two parts separately using the following differentiation rules:

`\boxed{\begin{aligned}&\underline{\sf Differentiation\;Rules}\\\\&\frac{\text{d}}{\text{d}x}(\arctan x)=(1)/(1+x^2)\\\\&\frac{\text{d}}{\text{d}x}\left(e^(f(x))\right)=f'(x)\cdot e^(f(x))\\\\\end{aligned}}`

Therefore:

`\frac{\text{d}y}{\text{d}u}=(1)/(2)\cdot (1)/(1+u^2)=(1)/(2(1+u^2))`

`\frac{\text{d}u}{\text{d}x}=4 \cdot e^(4x)=4e^(4x)`

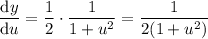
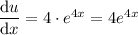
Put everything into the chain rule formula:

`\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}* \frac{\text{d}u}{\text{d}x}`

`\frac{\text{d}y}{\text{d}x}=(1)/(2(1+u^2))*4e^(4x)`

`\frac{\text{d}y}{\text{d}x}=(4e^(4x))/(2(1+u^2))`

`\frac{\text{d}y}{\text{d}x}=(2e^(4x))/(1+u^2)`

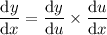
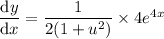
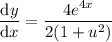
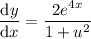
Substitute back
`u=e^(4x)`:

`\frac{\text{d}y}{\text{d}x}=(2e^(4x))/(1+\left(e^(4x)\right)^2)`

`\frac{\text{d}y}{\text{d}x}=(2e^(4x))/(1+e^(8x))`

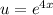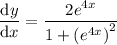
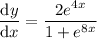
Therefore, the derivative of the given function is:

`\large\boxed{\boxed{f'(x)=(2e^(4x))/(1+e^(8x))}}`