Answer:
13.5 square units
Explanation:
The given circle with center Q has a circumference of 12π.
Using the formula C = 2πr for the circumference of a circle with radius r, we can find that the radius of circle Q:

Since points R and S are on the circumference of circle Q, then QR and QS are radii of the circle. As r = 6, then:
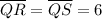
To find the area of the shaded region, we can subtract the area of the smaller right triangle AQB from the area of the larger right triangle RQS.
The area of a triangle is half the product of its base and height.
Therefore, the area of the larger triangle RQS is:
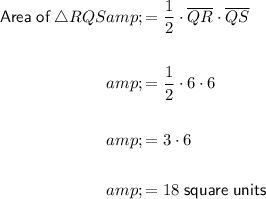
As A is the midpoint of
 and B is the midpoint of
and B is the midpoint of
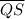 , then:
, then:
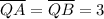
Therefore, the area of the smaller triangle AQB is:
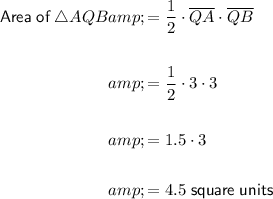
The area of the shaded region is the area of the smaller right triangle AQB subtracted from the area of the larger right triangle RQS:
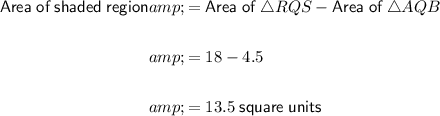
Therefore, the area of the shaded region is 13.5 square units.