Question

Q3.
Please help me as soon as possible.

Answer 1

42 units

Explanation:

Given:

ABCD is a parallelogram.

ABE is a equilateral triangle.

`\sf \overline{BE}=\overline{DE}=7`

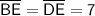
To find:

Perimeter of parallelogram.

Solution:

Since all sides of equilateral triangle are equal. so,

`\sf \overline{AB}=\overline{AE}=7`

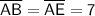
And

Oopposite side of the parallelogram are also equal,

So,

`\sf \overline{AB}=\overline{CD}=7`

`\sf \overline{BC}=\overline{AD}=\overline{AE}+\overline{ED}=7+7=14`

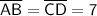
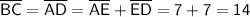
Now,

The perimeter of the parallelogram is equal to the sum of all sides:

`\begin{aligned} \textsf{The perimeter of the parallelogram} &\sf = \overline{AB}+\overline{BC}+\overline{CD}+\overline{AD} \\\\ &\sf = \textsf{Substitute the value:}\\\\ &\sf = 7+14+7+14\\\\ &\sf = 42 units \end{aligned}`

Therefore, the perimeter of a parallelogram is 42 units.