Question

What's the lateral area of the following cone? a. 55 cm² b. 511.23 cm² c. 189.75 cm² d. 110.02 cm²

Answer 1

The lateral area of the cone with a radius of 5 cm and a perpendicular height of 11 cm is approximately
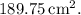`189.75 \, \text{cm}^2.`. This matches option c.

We can use the Pythagorean theorem to find the slant height (s) of the cone, given its radius (r) and perpendicular height (l).

The relationship between the slant height (s), radius (r), and perpendicular height (l) of a cone is:

`\[ s = √(r^2 + l^2) \]`

Given:

Radius (r) = 5 cm

Perpendicular height (l) = 11 cm

Let's find the slant height (s) first:

`\[ s = √(5^2 + 11^2) \]`

`\[ s = √(25 + 121) \]`

`\[ s = √(146) \]`

`\[ s \approx 12.083 \, \text{cm} \]`

Now that we have the slant height (s), we can calculate the lateral area of the cone using the formula:

`\[ \text{Lateral Area} = \pi r s \]`

Substituting the values:

`\[ \text{Lateral Area} = \pi * 5 * 12.083 \]`

`\[ \text{Lateral Area} = 60.415 \pi \]`

`\[ \text{Lateral Area} \approx 60.415 * 3.14 \]`

`\[ \text{Lateral Area} \approx 189.75 \, \text{cm}^2 \]`

Complete the image: