Question

Isosceles triangle ABC (AC=BC) has a base angle of 30 degrees and CD is the median to the base. How long are the legs of triangle ABC, if the sum of the perimeters of triangles ACD and triangle BCD is 20 cm more than the perimeter of triangle ABC?

Answer 1

• 
  `20cm`

Given :

• An isosceles triangle ABC wherein AC = BC with m∠A = m∠B = 30° and CD the median to the base AB.
• Sum of perimeter of ΔACD & ΔBCD = 20cm + Perimeter ΔABC

To find :

• Measure of AC & BC

Solution :

In ΔACD,

• m∠ADC = 90°
• m∠CAD = 30°
• m∠ACD= 180° - (90° + 30°) = 60°

from this,we can conclude that ,∠ACD = 2*∠CAD , thus, AC = 2CD.......(1)

In ΔBCD,

• m∠BDC = 90°
• m∠CBD = 30°

m∠BCD = 180° - (90° +30°) = 60°

from this, we can conclude that ,∠BCD = 2*CBD , thus , BC = 2CD......(2)

Now,

We know that,

• Perimeter of a Δ = sum of all it's sides
• Perimeter of ΔABC = AC + BC + AB or 2AC + AB
• Sum of perimeter of ΔACD & ΔBCD = (AC + AB/2 + CD) + (BC + AB/2 + CD) = (AC + AB/2 + CD) + (AC + AB/2 + CD) = 2AC + AB + 2CD

ATQ,

• 2AC + AB + 2CD = 20cm + 2AC + AB
• 2CD = 20cm

From equation (1),

• AC = 2CD
• AC = 20cm

and since AC = BC, thus,

• BC = 20cm

Thus, the measure of the legs of ΔABC is 20cm each.

Answer 2

20 cm

Explanation:

As the base angles of isosceles triangle ABC are 30°, and CD is the perpendicular bisector of the base AB, triangles ACD and ABD are congruent 30-60-90 right triangles.

This means that the sides of triangles ACD and ABD are in the ratio 1 : √3 : 2.

Let "x" be the shortest leg of the right triangles (CD).

Let "√3x" be the longest leg of the right triangles (AD and BD).

Let "2x" be the hypotenuse of the right triangle (AC and BC).

Therefore, the perimeters of triangles ABC, ACD and BCD can be expressed as:

`\begin{aligned}\textsf{Perimeter of $\triangle ABC$}&=2x + 2x + √(3)x+ √(3)x\\&=(4+2√(3))x\end{aligned}`

`\begin{aligned}\textsf{Perimeter of $\triangle ACD$}&=2x + √(3)x+ x\\&=(3+√(3))x\end{aligned}`

`\begin{aligned}\textsf{Perimeter of $\triangle BCD$}&=2x + √(3)x+ x\\&=(3+√(3))x\end{aligned}`

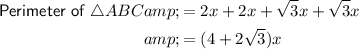
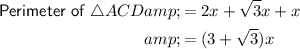
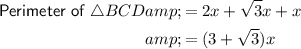
Given the sum of the perimeters of triangles ACD and BCD is 20 cm more than the perimeter of triangle ABC, then:

`\begin{aligned}\textsf{Perimeter of $\triangle ACD$}+\textsf{Perimeter of $\triangle BCD$}&=\textsf{Perimeter of $\triangle ABC$}+20\\\\(3+√(3))x+(3+√(3))x&=(4+2√(3))x+20\end{aligned}`

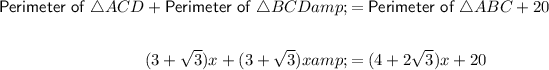
Solve the equation for x:

`\begin{aligned}(3+√(3))x+(3+√(3))x&=(4+2√(3))x+20\\\\(6+2√(3))x&=(4+2√(3))x+20\\\\(6+2√(3))x-(4+2√(3))x&=20\\\\(6+2√(3)-4-2√(3))x&=20\\\\2x&=20\\\\x&=10\end{aligned}`

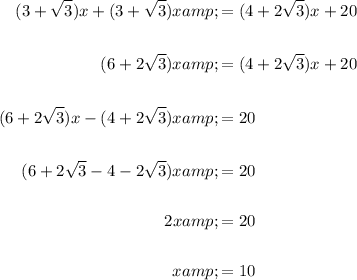
To determine the length of the legs of triangle ABC, substitute the found value of x into the expression for AC and BC:

`AC=BC=2x=2(10)=20`

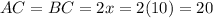
Therefore, the length of the legs AC and BC of triangle ABC are 20 cm.