Question

A railroad freight car, mass 15,000 kg, is allowed to coast along a level track at a speed of 2.0 m/s. It collides and couples with a 40,000-kg loaded second car, initially at rest and with brakes released. What percentage of the initial kinetic energy of the 15 000-kg car is preserved in the two-coupled cars after collision?

Answer 1

Approximately
`27.3\%`. (
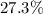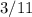`3/11` of the initial value.)

Step-by-step explanation:

Apply the following steps to find the percentage of kinetic energy preserved in this inelastic collision:

• Apply the conservation of momentum to find an expression for the velocity after the collision.
• Find an expression for the total kinetic energy after collision.
• Find an expression for the ratio between the final and initial value of kinetic energy.

When an object of mass
`m` moves at a velocity of
`v`, the momentum of a moving object would be
`m\, v`. The kinetic energy of that object would be
`(1/2)\, m\, v^(2)`.

Let
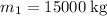`m_(1) = 15000\; {\rm kg}` denote the mass of the first train. Let
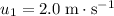`u_(1) = 2.0\; {\rm m\cdot s^(-1)}` denote the initial velocity of that train. The initial momentum of this train would be
`m_(1)\, u_(1)`.

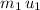Let
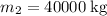`m_(2) = 40000\; {\rm kg}` denote the mass of the train that was initially not moving. Since the initial velocity of this train is
`0\!`, the initial momentum and kinetic energy of this train would both be
`0`.

Let
`v` denote the velocity of the two trains after the collision.

Total momentum before the collision was:

`p(\text{initial}) = m_(1)\, u_(1)`.

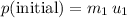Total momentum after the collision was:

`p(\text{final}) = m_(1)\, v + m_(2)\, v = (m_(1) + m_(2))\, v`.

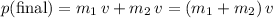By the conservation of momentum, total momentum should stay the same before and after the collision:

`p(\text{initial}) = p(\text{final})`.

`m_(1)\, u_(1) = (m_(1) + m_(2))\, v`.

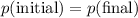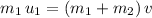Find an expression for the velocity
`v` of the two trains after the collision:

`\displaystyle v = \left((m_(1))/(m_(1) + m_(2))\right)\, u_(1)`.

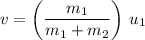The initial kinetic energy of the two trains, combined, would be:

`\displaystyle (\text{initial KE}) = (1)/(2)\, m_(1)\, {u_(1)}^(2)`.

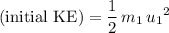The kinetic energy of the two trains after the collision would be:

`\begin{aligned} (\text{final KE}) &= (1)/(2)\, (m_(1) + m_(2))\, v^(2) \\ &= (1)/(2)\, (m_(1) + m_(2))\, {\left(\left((m_(1))/(m_(1) + m_(2))\right)\, u_(1)\right)}^(2) } \\ &= (1)/(2)\, (m_(1) + m_(2))\, \left(\frac{{m_(1)}^(2)}{(m_(1) + m_(2))^(2)}\, {u_(1)}^(2)\right) \\ &= (1)/(2)\, m_(1)\, {u_(1)}^(2) \, \left((m_(1))/(m_(1) + m_(2))\right)\end{aligned}`.

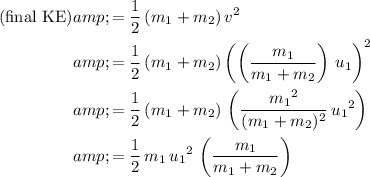Obtain an expression for the ratio
`(\text{final KE}) / (\text{initial KE})`:

`\begin{aligned}\frac{(\text{final KE})}{(\text{initial KE})} &= \frac{\displaystyle (1)/(2)\, m_(1)\, {u_(1)}^(2)\, \left((m_(1))/(m_(1) + m_(2))\right)}{\displaystyle (1)/(2)\, m_(1)\, {u_(1)}^(2)} = (m_(1))/(m_(1) + m_(2))\end{aligned}`.

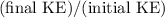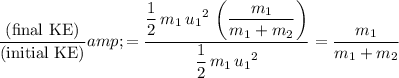Since
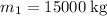`m_(1) = 15000\; {\rm kg}` and
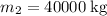`m_(2) = 40000\; {\rm kg}`, the value of this ratio would be:

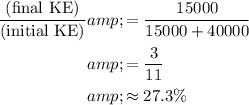`\begin{aligned}\frac{(\text{final KE})}{(\text{initial KE})} &= (15000)/(15000 + 40000)\\ &= (3)/(11) \\ &\approx 27.3\%\end{aligned}`.