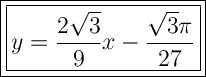Question

It is given that ∫f(x)dx = cos(x) + 1/2(sin(2x)) + 3.

f(x) = cos2x - sinx
Show that the equation of the normal to the curve y = f(x) is y = (2√3)(x)/9 - (√3π)/27 at the point where x = π/6.

Answer 1

`y=(2√(3))/(9)x-(√(3)\pi)/(27)`

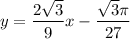
Explanation:

Given:

`\displaystyle \int f(x)\; \text{d}x=\cos(x)+(1)/(2)\sin (2x)+3`

`f(x)=\cos(2x)-\sin(x)`

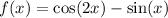
To find the equation of the normal to the curve y = f(x) at the point where x = π/6, we first need to differentiate f(x):

`f'(x)=-2\sin(2x)-\cos(x)`

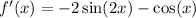
Now, find the slope of the tangent line at x = π/6 by substituting x = π/6 into the differentiated function:

`\begin{aligned}f'\left((\pi)/(6)\right)&=-2\sin\left(2\cdot (\pi)/(6)\right)-\cos\left((\pi)/(6)\right)\\\\&=-2\sin\left((\pi)/(3)\right)-\cos\left((\pi)/(6)\right)\\\\&=-2 \cdot (√(3))/(2)-(√(3))/(2)\\\\&=-(2√(3))/(2)-(√(3))/(2)\\\\&=-(3√(3))/(2)\end{aligned}`

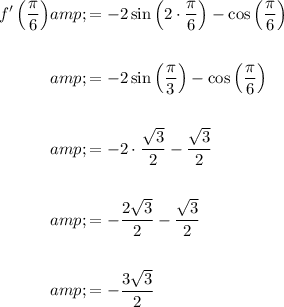
The slope of the normal line at a point on a curve is found by taking the negative reciprocal of the slope of the tangent line at the same point. Therefore, the slope (m) of the normal line at the point where x = π/6 is:

`m_(\sf normal)=-(1)/(f'\left((\pi)/(6)\right))=-(1)/(-(3√(3))/(2))=(2)/(3√(3))=(2\cdot √(3))/(3√(3)\cdot √(3))=(2√(3))/(9)`

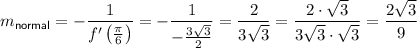
Find the y-coordinate of the point when x = π/6 by substituting x = π/6 into y = f(x):

`\begin{aligned}f\left((\pi)/(6)\right)&=\cos\left((2\pi)/(6)\right)-\sin\left((\pi)/(6)\right)\\\\&=\cos\left((\pi)/(3)\right)-\sin\left((\pi)/(6)\right)\\\\&=(1)/(2)-(1)/(2)\\\\&=0\end{aligned}`

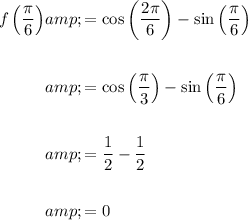
To find the equation of the normal, substitute the found slope and the point (π/6, 0) into the point-slope form of a linear equation:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\y-0&=(2√(3))/(9)\left(x-(\pi)/(6)\right)\\\\y&=(2√(3))/(9)x-(2√(3)\pi)/(54)\\\\y&=(2√(3))/(9)x-(√(3)\pi)/(27)\end{aligned}`

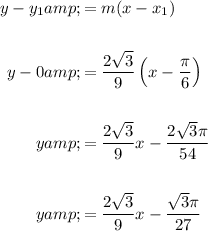
Therefore, the equation of the normal to the curve y = f(x) at the point where x = π/6 is:

`\Large\boxed{\boxed{y=(2√(3))/(9)x-(√(3)\pi)/(27)}}`