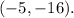Answer:
Explanation:
Let's break down the function
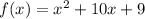 in simpler terms.
in simpler terms.
1. Start with the function
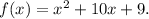
2. This is a quadratic function because it has a term with
 , and it's called quadratic because it represents a parabola.
, and it's called quadratic because it represents a parabola.
3. You can factor this quadratic expression as:
![\[f(x) = (x + 9)(x + 1)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ciyv3xxygt1ppiui1h6om4pzwjojqdhh6b.png)
This means that
 is the result of multiplying two simpler expressions
is the result of multiplying two simpler expressions
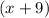 and
and
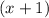 together.
together.
4. When you have a quadratic expression in this factored form, you can see where it equals zero. For this function, it equals zero when

5. These values of
 where
where
 are called the "roots" or "zeroes" of the function. They are the points where the parabola crosses the x-axis.
are called the "roots" or "zeroes" of the function. They are the points where the parabola crosses the x-axis.
6. The shape of the parabola depends on the coefficient of the
 term. In this case, since the coefficient is positive (1), the parabola opens upward.
term. In this case, since the coefficient is positive (1), the parabola opens upward.
7. The vertex of the parabola (the highest or lowest point) can be found using the formula
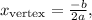 where
where
 is the coefficient of the
is the coefficient of the
 term (1) and
term (1) and
 is the coefficient of the
is the coefficient of the
 term (10). Plugging in these values, you find
term (10). Plugging in these values, you find
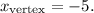
8. To find the corresponding
 -coordinate of the vertex, plug
-coordinate of the vertex, plug
 into the original function:
into the original function:
![\[f(-5) = (-5)^2 + 10(-5) + 9 = 25 - 50 + 9 = -16\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kjvnn2idx5xax72wn7k742tcgf54pw83y4.png)
9. So, the vertex of the parabola is at
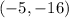 , and the function
, and the function
 describes this quadratic relationship. It represents a parabola that opens upward with its vertex at
describes this quadratic relationship. It represents a parabola that opens upward with its vertex at