Answer:
So, the derivative of the function
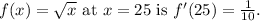
Now, we have the slope of the tangent line to the graph of the function at
 . The slope is
. The slope is
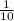 .
.
Explanation:
To find the derivative of the function
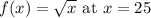 , we'll use the definition of the derivative:
, we'll use the definition of the derivative:
![\[f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2g4vw7sva28unvr9yrnj5l0v1i4vf65k6b.png)

![\[f'(x) = \lim_(h \to 0) (√(x + h) - √(x))/(h)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7ypy05sdhs2psn15y22ftr0xk7cy8wziyt.png)
Now, we'll calculate the derivative using this limit:
![\[f'(x) = \lim_(h \to 0) (√(x + h) - √(x))/(h) \cdot (√(x + h) + √(x))/(√(x + h) + √(x))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8cfykh060sif241pkby348iz7td4ez07qw.png)
This step involves multiplying the numerator and denominator by the conjugate of the numerator to eliminate the square root in the numerator. This is a common technique when dealing with square root functions.
Simplify the expression:
![\[f'(x) = \lim_(h \to 0) ((x + h) - x)/(h(√(x + h) + √(x)))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2wd843pxcmvy7ri4kot2rsfl7ngvtxfphw.png)
Now, simplify the numerator:
![\[f'(x) = \lim_(h \to 0) (h)/(h(√(x + h) + √(x)))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f2geib2jz94zfwaagwj4g9je2ft6pi5s3x.png)
Notice that we can cancel \(h\) in the numerator and denominator:
![\[f'(x) = \lim_(h \to 0) (1)/(√(x + h) + √(x))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ttpa41ddxd9kyh4n18fw2prss0forho6mm.png)
Now, evaluate the limit as
 approaches 0:
approaches 0:
![\[f'(25) = (1)/(√(25 + 0) + √(25))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/thxk4wjsnc89ljvl0tp1iyzqq1ptszuvzr.png)
![\[f'(25) = (1)/(√(25) + √(25))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zyxdh6de0qt5tmqwwkoo2jipbtr4z6i28x.png)
![\[f'(25) = (1)/(5 + 5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/po4yhshhz7lnq19gtf1l517a0vvpeqfdt5.png)
![\[f'(25) = (1)/(10)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w7w9d01rhkc358rzaf0u5hhhfpds654arh.png)
So, the derivative of the function
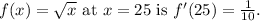
Now, we have the slope of the tangent line to the graph of the function at
 . The slope is
. The slope is
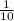 .
.