Answer:
x = 1 or -2
Explanation:
Given the equation:
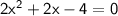
We can factor out the common factor of 2 from all the terms: x = 1 or -2.
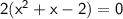
Now, let's simplify further by factoring the quadratic expression by middle term factorization:
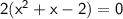
We can write it as:
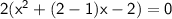

Now, factor by grouping:

Now, factor out common terms from each group:
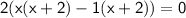
Now, we have a common factor of (x + 2) in both terms:
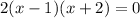
So, the quadratic equation in standard form is:

Either,
(x-1)=0
x=1
or
(x+2)=0
x=-2,
Therefore, x = 1 or -2.